
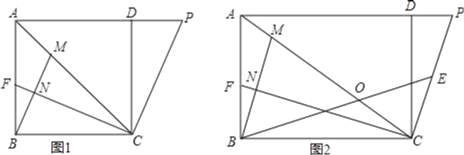
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDжаЃЌЕуPЮЊADбгГЄЯпЩЯвЛЕуЃЌСЌНгACЁЂCPЃЌЙ§ЕуCзїCFЁЭCPНЛгкCЃЌНЛABгкЕуFЃЌЙ§ЕуBзїBMЁЭCFгкЕуNЃЌНЛACгкЕуMЃЎ
ЃЈ1ЃЉШєAP=![]() ACЃЌBC=4ЃЌЧѓSЁїACPЃЛ
ACЃЌBC=4ЃЌЧѓSЁїACPЃЛ
ЃЈ2ЃЉШєCPЉBM=2FNЃЌЧѓжЄЃКBC=MCЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЦфЫћЬѕМўВЛБфЕФЧщПіЯТЃЌНЋЁАе§ЗНаЮABCDЁБИФЮЊЁАОиаЮABCDЁБЃЌЧвABЁйBCЃЌAC=APЃЌШЁCPжаЕуEЃЌСЌНгEBЃЌНЛACгкЕуOЃЌВТЯыЃКЁЯAOBгыЁЯABMжЎМфгаКЮЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ7![]() ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉЁЯAOB=3ЁЯABMЃЌРэгЩМћНтЮіЃЎ
ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉЁЯAOB=3ЁЯABMЃЌРэгЩМћНтЮіЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩе§ЗНаЮЕФаджЪЕУГіAB=BC=CD=4ЃЌЁЯADC=ЁЯCDP=ЁЯABC=ЁЯBCD=90ЁуЃЌгЩЙДЙЩЖЈРэЧѓГіACЃЌЕУГіAPЃЌМДПЩЧѓГіSЁїACPЃЛ
ЃЈ2ЃЉдкCFЩЯНиШЁNG=FNЃЌСЌНгBGЃЌдђCFЉCG=2FNЃЌжЄГіЁЯBCF=ЁЯDCPЃЌгЩASAжЄУїЁїBCFЁеЁїDCPЃЌЕУГіCF=CPЃЌжЄГіCG=BMЃЌгЩSASжЄУїЁїABMЁеЁїBCGЃЌЕУГіЁЯAMB=ЁЯBGCЃЌвђДЫЁЯBMC=ЁЯBGFЃЌгЩЯпЖЮДЙжБЦНЗжЯпЕФаджЪЕУГіBF=BGЃЌЕУГіЁЯBFG=ЁЯBGFЃЌвђДЫЁЯBMC=ЁЯCBMЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉСЌНгAEЃЌЯШжЄГіЁЯBCA=2ЁЯPAEЃЌдйжЄУїAЁЂDЁЂEЁЂCЫФЕуЙВдВЃЌгЩдВжмНЧЖЈРэЕУГіЁЯDCP=ЁЯPAEЃЌЕУГіЁЯBCF=ЁЯPAEЃЌжЄГіЁЯBCA=2ЁЯABMЃЌШЛКѓгЩШ§НЧаЮЕФЭтНЧаджЪМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЁпЫФБпаЮABCЪЧе§ЗНаЮЃЌ
ЁрADЁЮBCЃЌAB=BC=CD=4ЃЌЁЯADC=ЁЯCDP=ЁЯABC=ЁЯBCD=90ЁуЃЌ
ЁрAC=![]() =4
=4![]() ЃЌ
ЃЌ
ЁрAP=![]() AC=
AC=![]() ЁС4
ЁС4![]() =
=![]() ЃЌ
ЃЌ
ЁрSЁїACP=![]() APЁСCD=
APЁСCD=![]() ЁС
ЁС![]() ЁС4=7
ЁС4=7![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкCFЩЯНиШЁNG=FNЃЌСЌНгBGЃЌШчЭМ1ЫљЪОЃК
дђCFЉCG=2FNЃЌ
ЁпCFЁЭCPЃЌ
ЁрЁЯPCF=90ЁуЃЌ
ЁрЁЯBCF=ЁЯDCPЃЌ
дкЁїBCFКЭЁїDCPжаЃЌ ЃЌ
ЃЌ
ЁрЁїBCFЁеЁїDCPЃЈASAЃЉЃЌ
ЁрCF=CPЃЌ
ЁпCPЉBM=2FNЃЌ
ЁрCG=BMЃЌ
ЁпЁЯABC=90ЁуЃЌBMЁЭCFЃЌ
ЁрЁЯABM=ЁЯBCGЃЌЁЯBFG=ЁЯCBMЃЌ
дкЁїABMКЭЁїBCGжаЃЌ ЃЌ
ЃЌ
ЁрЁїABMЁеЁїBCGЃЈSASЃЉЃЌ
ЁрЁЯAMB=ЁЯBGCЃЌ
ЁрЁЯBMC=ЁЯBGFЃЌ
ЁпGN=FNЃЌBMЁЭCFЃЌ
ЁрBF=BGЃЌ
ЁрЁЯBFG=ЁЯBGFЃЌ
ЁрЁЯBMC=ЁЯCBMЃЌ
ЁрBC=MCЃЛ
ЃЈ3ЃЉЁЯAOB=3ЁЯABMЃЛРэгЩШчЯТЃК
СЌНгAEЃЌШчЭМ2ЫљЪОЃК
ЁпAC=APЃЌEЪЧCPЕФжаЕуЃЌ
ЁрAEЁЭCPЃЌЁЯPAE=ЁЯCAEЃЌ
ЁпADЁЮBCЃЌ
ЁрЁЯBCA=ЁЯPAC=2ЁЯPAEЃЌ
ЁпCFЁЭCPЃЌ
ЁрЁЯPCF=90ЁуЃЌ
ЁрЁЯBCF=ЁЯDCPЃЌ
ЁпЁЯADC=ЁЯAEC=90ЁуЃЌ
ЁрAЁЂDЁЂEЁЂCЫФЕуЙВдВЃЌ
ЁрЁЯDCP=ЁЯPAEЃЌ
ЁрЁЯBCF=ЁЯPAEЃЌ
гжЁпЁЯABM=ЁЯBCFЃЌ
ЁрЁЯABM=ЁЯBCF=ЁЯPAEЃЌ
ЁрЁЯBCA=2ЁЯABMЃЌ
ЁпЁЯAOB=ЁЯBCF+ЁЯBCAЃЌ
ЁрЁЯAOB=3ЁЯABMЃЎ





| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌЁЯACB=90Ёу,ЁЯCAB=30ЁуЃЌЁїABDЪЧЕШБпШ§НЧаЮЃЌЙ§ЕуCзїCF//BD,НЛABгкЕуEЃЌНЛADгкЕуFЃЎ

ЃЈ1ЃЉЧѓжЄ:ЁїAEFЁеЁїBECЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌНЋЫФБпаЮACBDелЕўЃЌЪЙDгыCжиКЯЃЌHKЮЊелКлЃЌШчЭМ2ЃЌЧѓsinЁЯACHЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
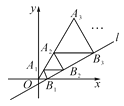
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпlЃК![]() гыxжсНЛгкЕуB1ЃЌвдOB1ЮЊБпГЄзїЕШБпЁїA1OB1ЃЌЙ§ЕуA1зїA1B2ЦНаагкxжсЃЌНЛжБЯпlгкЕуB2ЃЌвдA1B2ЮЊБпГЄзїЕШБпЁїA2A1B2ЃЌЙ§ЕуA2зїA2B3ЦНаагкxжсЃЌНЛжБЯпlгкЕуB3ЃЌвдA2B3ЮЊБпГЄзїЕШБпЁїA3A2B3ЃЌЁЃЌдђЕуA2 018ЕФКсзјБъЪЧ_____________.
гыxжсНЛгкЕуB1ЃЌвдOB1ЮЊБпГЄзїЕШБпЁїA1OB1ЃЌЙ§ЕуA1зїA1B2ЦНаагкxжсЃЌНЛжБЯпlгкЕуB2ЃЌвдA1B2ЮЊБпГЄзїЕШБпЁїA2A1B2ЃЌЙ§ЕуA2зїA2B3ЦНаагкxжсЃЌНЛжБЯпlгкЕуB3ЃЌвдA2B3ЮЊБпГЄзїЕШБпЁїA3A2B3ЃЌЁЃЌдђЕуA2 018ЕФКсзјБъЪЧ_____________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
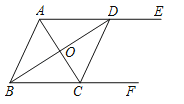
ЁОЬтФПЁПШчЭМЃЌAEЁЮBFЃЌACЦНЗжЁЯBAEЃЌЧвНЛBFгкЕуCЃЌBDЦНЗжЁЯABFЃЌЧвНЛAEгкЕуDЃЌСЌНгCDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧСтаЮЃЛ
ЃЈ2ЃЉШєЁЯADB=30ЁуЃЌBD=6ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊЃВЕФе§ЗНаЮABCDЕФЖЅЕуAдкЃљжсЩЯЃЌЖЅЕуDдкЗДБШР§КЏЪ§yЃНЃЈx>0ЃЉЕФЭМЯёЩЯЃЌвбжЊЕуBЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЃЉЃЌдђkЕФжЕЮЊЃЈ ЃЉ

AЃЎ10 BЃЎ8 CЃЎ6 DЃЎ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
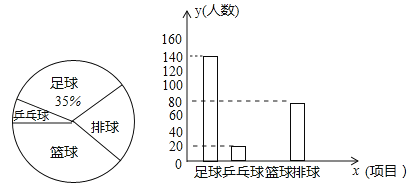
ЁОЬтФПЁПФГаЃЮЊЬсИпбЇЩњЩэЬхЫижЪЃЌОіЖЈПЊеЙзуЧђЁЂРКЧђЁЂЬЈЧђЁЂЦЙХвЧђЫФЯюПЮЭтЬхг§ЛюЖЏЃЌВЂвЊЧѓбЇЩњБиаыВЂЧвжЛФмбЁдёвЛЯюЃЎЮЊСЫНтбЁдёИїжжЬхг§ЛюЖЏЯюФПЕФбЇЩњШЫЪ§ЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂЛцжЦГівдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭГМЦЭМЛиД№ЯТСаЮЪЬтЃЎЃЈвЊЧѓаДГіМђвЊЕФНтД№Й§ГЬЃЉ
ЃЈ1ЃЉетДЮЛюЖЏвЛЙВЕїВщСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉШєИУбЇаЃзмШЫЪ§ЪЧ1300ШЫЃЌЧыЙРМЦбЁдёРКЧђЯюФПЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕуFДгСтаЮABCDЕФЖЅЕуAГіЗЂЃЌбиAЁњDЁњBвд1cm/sЕФЫйЖШдШЫйдЫЖЏЕНЕуBЃЌЭМ2ЪЧЕуFдЫЖЏЪБЃЌЁїFBCЕФУцЛ§yЃЈcm2ЃЉЫцЪБМфxЃЈsЃЉБфЛЏЕФЙиЯЕЭМЯѓЃЌдђaЕФжЕЮЊЃЈЁЁЁЁЃЉ

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпx=2ЃЌгыxжсЕФвЛИіНЛЕузјБъЃЈ4ЃЌ0ЃЉЃЌЦфВПЗжЭМЯѓШчЭМЫљЪОЃЌЯТСаНсТлЃКЂйХзЮяЯпЙ§дЕуЃЛЂкaЉb+cЃМ0ЃЛЂл4a+b+c=0ЃЛЂмХзЮяЯпЕФЖЅЕузјБъЮЊЃЈ2ЃЌbЃЉЃЛЂнЕБxЃМ1ЪБЃЌyЫцxдіДѓЖјдіДѓЃЎЦфжаНсТле§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
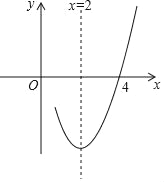
A. ЂйЂкЂл B. ЂйЂмЂн C. ЂйЂлЂм D. ЂлЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќаЉФъРДЃЌЁАаЃдААВШЋЁБЪмЕНШЋЩчЛсЕФЙуЗКЙизЂЃЌЮЊСЫСЫНтбЇЩњЖдгкАВШЋжЊЪЖЕФСЫНтГЬЖШЃЌбЇаЃВЩгУЫцЛњГщбљЕФЕїВщЗНЪНЃЌИљОнЪеМЏЕНЕФаХЯЂНјааЭГМЦЃЌЛцжЦСЫЯТУцСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎ
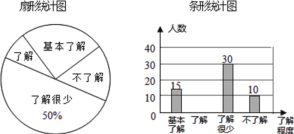
ЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВга________ШЫЃЎ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєДгЖдаЃдААВШЋжЊЪЖДяЕНСЫЁАСЫНтЁБГЬЖШЕФ3ИіХЎЩњКЭ2ИіФаЩњжаЫцЛњГщШЁ2ШЫВЮМгаЃдААВШЋжЊЪЖОКШќЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГіЧЁКУГщЕН1ИіФаЩњКЭ1ИіХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com