
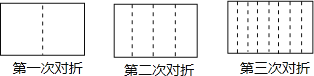
【题目】将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,
(1)折一折,数一数,连续对折四次后,可以得到多少条折痕?
(2)想一想,如果对折n次,可以得到多少条折痕?
(3)如果能对折10次,可以得到多少条折痕?
(4)如果对折n次,可以得到多少个一样大小的小长方形?
【答案】(1)15;(2)2n﹣1;(3)1023;(4)2n.
【解析】
(1)对前三次对折可经发现每对折1次把纸分成的部分是上一次的2倍,折痕数是所分成的部分数少1,据此可求出第4次的折痕;
(2)根据(1)对折规律求出对折n次得到的部分数,然后减1即可得到折痕条数;
(3)把n=10代入(2)中的式子即可计算出结果;
(4)对折n次得到的部分数就是小长方形的个数.
解:由图可知,第1次对折,把纸分成2部分,1条折痕,
第2次对折,把纸分成4部分,3条折痕,
第3次对折,把纸分成8部分,7条折痕,
(1)第4次对折,把纸分成16部分,15条折痕,
(2)依此类推,第n次对折,把纸分成2n部分,2n﹣1条折痕.
(3)第10次对折,把纸分成210部分,210﹣1=1023条折痕;
(4)对折n次,可以得到2n个一样大小的小长方形


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,①求边CP的长;②求边AB的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为< x >,即已知n为正整数,如果n-![]() ≤x<n+
≤x<n+![]() ,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=
,那么< x >=n.例如:< 0 >=< 0.48 >=0,< 0.64 >=< 1.493 >=1,< 2 >=2,< 3.5 >=< 4.12 >=4,…则满足方程< x >=![]() 的非负实数x的值为____.
的非负实数x的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4.5>=5,<-1.5>=-1.解决下列问题.
(1)[-4.5]=_____;<3.5>=________;
(2)若[x]=2,则x的取值范围是________;若<y>=-1,则y的取值范围是_______.
(3)若![]() ,则x为_________.
,则x为_________.
(4)已知x、y满足方程组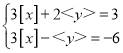
![]() ,求x、y的取值范围.
,求x、y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(观察探索)用“<”、“>”或“=”完成以下填空,并观察两边算式,探索规律:
![]()
![]()
![]()
![]()
(猜想证明)请用一个含字母a、b的式子表示上以规律,并证明结论的正确性;
(应用拓展)比较代数式m2-3mn+1与mn-4n2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上
与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上![]() 轴子点D,交直线AC于点E.
轴子点D,交直线AC于点E.

(1) ![]()
(2)过点P作PF⊥AC于点F.求当△PEF的周长取最大值时点P的坐标.
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求对应的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com