
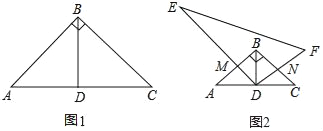
【题目】特例探究:如图①,已知在△ABC中,AB=BC,∠ABC=90°,D为AC边的中点,连接BD,判断△ABD是什么三角形,并说明理由.
归纳证明:如图②,已知在△ABC中,AB=BC,∠ABC=90°,D为AC边的中点,连接BD,把Rt△DEF的直角顶点D放在AC的中点上,DE交AB于M,DF交BC于N.证明:DM=DN.
拓展应用:在图②,AC=4,其他条件都不发生变化,请直接写出Rt△DEF与△ABC的重叠部分的面积.
【答案】特例探究:△ABD是等腰直角三角形,理由见解析;归纳证明:证明见解析;拓展应用:2.
【解析】
特例探究:根据等腰直角三角形的性质和三线合一,直接证得△ABD是等腰直角三角形即可;
归纳证明:证得△DMA≌△DNB(ASA),即可得出答案;
拓展应用:由归纳证明可知△DMA≌△DNB(ASA),同理可得△BDM≌△DCN(ASA),由此得出Rt△DEF与△ABC的重叠部分(四边形DMBN的面积是△ABC面积的一半,即可得出结论.
特例探究:△ABD是等腰直角三角形.理由如下:
∵AB=BC,∠ABC=90°,∴△ABC为等腰直角三角形.
∵D为AC边的中点,∴BD⊥AC,AD=CD=![]() AC,BD=
AC,BD=![]() AC,∴AD=BD,∴△ABD是等腰直角三角形.
AC,∴AD=BD,∴△ABD是等腰直角三角形.
归纳证明:∵AB=CB,∴∠A=∠C=45°.
∵D是AC的中点,∴DA=DC=BD,∠DBN=45°,BD⊥AC,∴∠ADB=∠ADM+∠BDM=90°,∴∠A=∠DBN.
∵∠EDF=90°,∴∠BDN+∠BDM=90°,∴∠ADM=∠BDN.
在△DMA和△DBN中,∵∠ADM=∠BDN,AD=BD,∠A=∠DBN,∴△DMA≌△DNB(ASA),∴DM=DN.
拓展应用:∵AC=4,△ABC为等腰直角三角形,∴AB=BC=![]() ,由归纳证明,可知△DMA≌△DNB(ASA),同理可得△BDM≌△DCN(ASA),∴S四边形DMBN=S△BDM+S△DBN=
,由归纳证明,可知△DMA≌△DNB(ASA),同理可得△BDM≌△DCN(ASA),∴S四边形DMBN=S△BDM+S△DBN=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图. 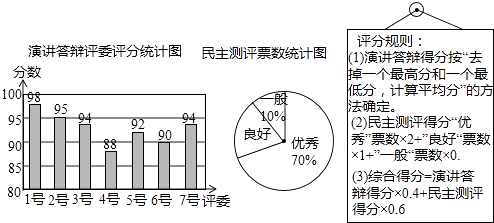
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=k(x+1)(x﹣ ![]() )与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
)与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是数轴的一部分,其单位长度为a,已知△ABC中,AB=3a,BC=4a,AC=5a. ![]()
(1)用直尺和圆规作出△ABC(要求:使点A,C在数轴上,保留作图痕迹,不必写出作法);
(2)记△ABC的外接圆的面积为S圆 , △ABC的面积为S△ , 试说明 ![]() >π.
>π.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个边长为a的大正方形,剪去一个边长为b的小正方形,即图①称之为“前世”,然后再剪拼成一个新长方形如图②称之为“今生”,请你解答下面的问题:

(1)“前世”图①的面积与“今生”图②新长方形的面积 ;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为: ,标明“今生”图②新长方形的长为 、宽为 ,面积为: .
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为: .
(4)请你根据(3)题中乘法公式,计算:2.001×1.999.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,然后按要求解答问题:
例题:已知二次三项式 ![]() 有一个因式是
有一个因式是 ![]() ,求另一个因式以及
,求另一个因式以及 ![]() 的值.
的值.
解法一:设另一个因式为 ![]() ,
,
得 ![]() ,
,
则 ![]() ,
,
![]() ,
,
解得 ![]() ,
,
![]() 另一个因式为
另一个因式为 ![]() ,
,![]() 的值为
的值为 ![]() .
.
解法二:∵二次三项式 x2-4x+m 有一个因式是 (x+3),
∴当x+3=0,即x=-3时,x2-4x+m=0.
把x=-3代入x2-4x+m=0,
得m=-21,
而x2-4x-21=(x+3)(x-7).
问题:分别仿照以上两种方法解答下面问题:
(1)已知二次三项式 ![]() 有一个因式是
有一个因式是 ![]() ,求另一个因式以及
,求另一个因式以及 ![]() 的值.
的值.
解法一: 解法二:
(2)直接回答:
已知关于x的多项式 2x3![]() (3
(3![]() k)x2
k)x2![]() 2x
2x![]() 1有一个因式是
1有一个因式是 ![]() 1,则k的值为_________.
1,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠B=60°,边AB=BC=8cm,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是每秒1cm,点Q运动的速度是每秒2cm,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
解答下列问题:
(1)AP= ,BP= ,BQ= .(用含t的代数式表示,t≤4)
(2)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(3)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
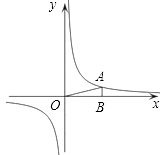
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y= ![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 ![]() .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y= ![]() 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y= ![]() 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年5月20日是第22个中国学生营养日,某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如图).根据信息,解答下列问题. 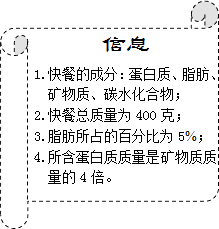
(1)求这份快餐中所含脂肪质量;
(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,求其中所含碳水化合物质量的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com