
【题目】综合与探究
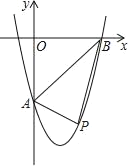
如图,已知抛物线y=ax2﹣3x+c与y轴交于点A(0,﹣4),与x轴交于点B(4,0),点P是线段AB下方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点的坐标;
(2)当点P移动到抛物线的什么位置时,∠PAB=90°求出此时点P的坐标;
(3)当点P从点A出发,沿线段AB下方的抛物线向终点B移动,在移动中,设点P的横坐标为t,△PAB的面积为S,求S关于t的函数表达式,并求t为何值时S有最大值,最大值是多少?
【答案】(1)y=x2﹣3x﹣4,![]() (2)(2,﹣6);(3)当t=2时,S取得最大值,最大值为8.
(2)(2,﹣6);(3)当t=2时,S取得最大值,最大值为8.
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出抛物线的解析式,再利用配方法即可求出抛物线的顶点坐标;
(2)过点P作PQ⊥OA于点Q,由OA=OB结合∠PAB=90°可得出∠PAQ=45°,进而可得出AQ=PQ,设点P的坐标为(m,m2﹣3m﹣4),由点A的坐标结合AQ=PQ可得出关于m的一元二次方程,解之取其正值即可得出结论;
(3)根据点A,B的坐标,利用待定系数法即可求出直线AB的解析式,过点P作PM⊥x轴,垂足为点M,由点P的横坐标为t可得出点P,M的坐标,进而可得出PM的长,由S△PAB=S梯形OAPM+S△PBM﹣S△AOB可得出S关于t的函数表达式,再利用二次函数的性质即可解决最值问题.
(1)将A(0,﹣4),B(4,0)代入y=ax2﹣3x+c,得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为y=x2﹣3x﹣4.
∵![]() ,
,
∴抛物线的顶点坐标为![]() .
.
(2)过点P作PQ⊥OA于点Q,如图1所示.

∵OA=OB,
∴∠OAB=45°.
又∵∠PAB=90°,
∴∠PAQ=45°,
∴AQ=PQ.
设点P的坐标为(m,m2﹣3m﹣4),
∴m=﹣4﹣(m2﹣3m﹣4),
解得:m1=0(舍去),m2=2,
∴点P的坐标为(2,﹣6).
(3)设直线AB的解析式为y=kx+b(k≠0),
将A(0,﹣4),B(4,0)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=x﹣4.
过点P作PM⊥x轴,垂足为点M,如图2所示.

∵点P的坐标为(t,t2﹣3t﹣4),
∴点M的坐标为(t,0),
∴PM=﹣t2+3t+4
∴S△PAB=S梯形OAPM+S△PBM﹣S△AOB,
=![]() (OA+PM)OM+
(OA+PM)OM+![]() PMBM﹣
PMBM﹣![]() OAOB,
OAOB,
=![]() [4+(﹣t2+3t+4)]t+
[4+(﹣t2+3t+4)]t+![]() (﹣t2+3t+4)(4﹣t)﹣
(﹣t2+3t+4)(4﹣t)﹣![]() ×4×4,
×4×4,
=﹣2t2+8t,
即S=﹣2t2+8t(0≤t≤4).
S=﹣2t2+8t=﹣2(t﹣2)2+8,
∵﹣2<0,
∴当t=2时,S取得最大值,最大值为8.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,抛物线的对称轴
是抛物线的顶点,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(1)求经过![]() ,
,![]() ,
,![]() 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;
(2)点![]() 是线段
是线段![]() 上一点,当
上一点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 为抛物线上一动点,
为抛物线上一动点,![]() 为
为![]() 轴上一动点,
轴上一动点,![]() 为直线
为直线![]() 上一动点,当以
上一动点,当以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形时,请求出点
为顶点的四边形是正方形时,请求出点![]() 的坐标.
的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=kx+b(k≠0)与反比例函数y![]() 的图象的一个交点为M(1,m).
的图象的一个交点为M(1,m).
(1)求m的值;
(2)直线l与x轴交于点A,与y轴交于点B,连接OM,设△AOB的面积为S1,△MOB的面积为S2,若S1≥3S2,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
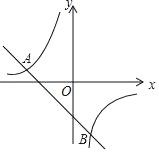
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数![]() 的图象相交于点A(﹣4,2),B(n,﹣4)
的图象相交于点A(﹣4,2),B(n,﹣4)
(1)求一次函数和反比例函数的表达式;
(2)观察图象,直接写出不等式y1<y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,其中
,其中![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
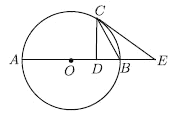
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)如图,点![]() 在
在![]() 上,且满足
上,且满足![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
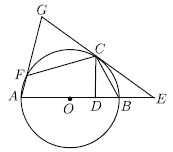
①试探究线段![]() 与
与![]() 之间满足的数量关系.
之间满足的数量关系.
②若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经)是我国传统数学的重要著作之一,其中记载的“荡杯问题”非常有趣.原题是今有妇人河上荡杯,津吏问日:“杯何以多?”妇人日:“有客.”津吏日:“客几何?”妇人日:“两人共饭,三人共羹,四人共肉,凡用杯六十五.不知客几何?”
大意:一个妇女在河边洗碗,河官问:“洗多少碗?有多少客?”妇女答:“洗![]() 只碗,客人二人.共用一只饭碗,三人共用一只汤碗,四人共用一只肉碗.问:有多少客人用餐?”请解答上述问题.
只碗,客人二人.共用一只饭碗,三人共用一只汤碗,四人共用一只肉碗.问:有多少客人用餐?”请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 为常数).
为常数).
(1)求证:不论![]() 为何值,该二次函数的图像与
为何值,该二次函数的图像与![]() 轴总有公共点.
轴总有公共点.
(2)求证:不论![]() 为何值,该二次函数的图像的顶点都在函数
为何值,该二次函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)已知点![]() 、
、![]() ,线段
,线段![]() 与函数
与函数![]() 的图像有公共点,则
的图像有公共点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com