练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．设a，b为实数，且满足（a-3）2+（b-1）2=0，求$\sqrt{\frac{b}{a}}$的值．

    分析 首先由非负数的非负性，求得a与b的值，再代入$\sqrt{\frac{b}{a}}$，化简即可求得答案．

    解答 解：∵（a-3）2+（b-1）2=0，
    ∴a-3=0，b-1=0，
    解得：a=3，b=1，
    ∴$\sqrt{\frac{b}{a}}$=$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$．

    点评 此题考查了二次根式的化简以及非负数的非负性．注意非负数的和等于0，则每项都等于0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

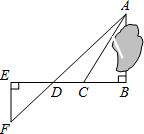    11．为了测量被池塘隔开的A、B两点之间的距离，根据实际情况，作出如图所示的图形，其中AB⊥BE，EF⊥BE，AF交BE于D，C在BD上，有四位同学分别测量出相关数据：甲为“BC、∠ACB”；乙为“CD、∠ACB”；丙为“EF、DE、BD”；丁为“DE、DC、BC”．根据所测数据，不能求出A、B间距离的是乙和丁同学．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列条件中，能判断△ABC∽△A′B′C′的有（　　）
    ①∠A=45°，AB=24，AC=30，∠A′=45°，A′B′=32，A′C′=40；
    ②AB=6，BC=7.5，AC=12，A′B′=10，B′C′=12.5，A′C′=20；
    ③∠A=47°，AB=1.5，AC=2，∠A′=47°，A′B′=2.8，B′C′=2.1．
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．用恰当的方法解下列方程．
    （1）（x+3）（x-4）=-12；
    （2）（2x-1）2-4（2x-1）=12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

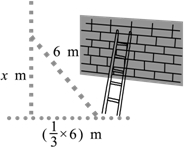    16．生活表明，靠墙摆放梯子时，若梯子底端离墙的距离为梯子长度的三分之一，则梯子比较稳定．现有一长度为6m的梯子，当梯子稳定摆放时，它的顶端最多能到达多高？（精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：
    （1）9$\sqrt{3}$-7$\sqrt{12}$+5$\sqrt{48}$；
    （2）$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

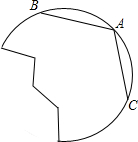    13．将图中的破轮子复原，已知弧上三点A，B，C．
    （1）画出该轮的圆心；
    （2）若△ABC是等腰三角形，底边BC=16cm，腰AB=10cm，求圆片的半径R．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

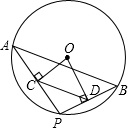    10．如图，点A，B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A，B不重合），连接AP，PB，过点O分别作OC⊥AP于点C，OD⊥PB于点D，则CD=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知△ABC中，∠A是锐角，AB=c，BC=a，CA=b．

    （1）当∠A=30°，b=6，c=3时，S△ABC=4.5，$\frac{1}{2}$bc•sinA=4.5；
    （2）当∠A=45°，b=6，c=3时，S△ABC=$\frac{9\sqrt{2}}{2}$，$\frac{1}{2}$bc•sinA=$\frac{9\sqrt{2}}{2}$；
    （3）当∠A=60°，b=4，c=3时，S△ABC=3$\sqrt{3}$，$\frac{1}{2}$bc•sinA=3$\sqrt{3}$；
    （4）根据（1），（2），（3）题的解答，猜想S△ABC与$\frac{1}{2}$bc•sinA的大小关系，并给出证明．

    查看答案和解析>>

    同步练习册答案