
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
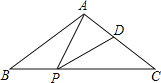
(1)求证:ACCD=CPBP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
【答案】(1)见解析;(2)BP=![]() .
.
【解析】
试题分析:(1)易证∠APD=∠B=∠C,从而可证到△ABP∽△PCD,即可得到![]() =
=![]() ,即ABCD=CPBP,由AB=AC即可得到ACCD=CPBP;
,即ABCD=CPBP,由AB=AC即可得到ACCD=CPBP;
(2)由PD∥AB可得∠APD=∠BAP,即可得到∠BAP=∠C,从而可证到△BAP∽△BCA,然后运用相似三角形的性质即可求出BP的长.
解:(1)∵AB=AC,∴∠B=∠C.
∵∠APD=∠B,∴∠APD=∠B=∠C.
∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴![]() =
=![]() ,
,
∴ABCD=CPBP.
∵AB=AC,
∴ACCD=CPBP;
(2)∵PD∥AB,∴∠APD=∠BAP.
∵∠APD=∠C,∴∠BAP=∠C.
∵∠B=∠B,
∴△BAP∽△BCA,
∴![]() =
=![]() .
.
∵AB=10,BC=12,
∴![]() =
=![]() ,
,
∴BP=![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B在⊙O上,点C在⊙O外,连接AB和OC交于D,且OB⊥OC,AC=CD.
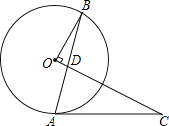
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OC=13,OD=1,求⊙O的半径及tanB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
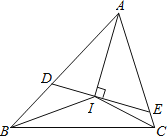
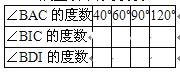
(1)请你通过画图、度量,填写右上表(图画在草稿纸上,并尽量画准确)
(2)从上表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线y=x2﹣4先向右平移两个单位,再向上平移两个单位,得到的抛物线的解析式是( )
A. y=(x+2)2+2
B. y=(x﹣2)2﹣2
C. y=(x﹣2)2+2
D. y=(x+2)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
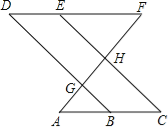
【题目】如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
则∠A=∠F,请说明理由.
解:∵∠AGB=∠EHF
∠AGB= (对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC
∴∠ =∠DBA ( 两直线平行,同位角相等)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com