
分析 根据题意得出菱形的面积与周长,进而利用勾股定理得出BE的长,即可得出EC的长.
解答  解:如图1所示:
解:如图1所示:
∵一个底面为菱形的直棱柱,高为10cm,体积为150cm2,
∴菱形的面积为:15cm2,
∵棱柱侧面展开图的面积为200cm2,
∴菱形的周长为20cm,
∴菱形的边长为:5cm,
过点A作AE⊥CB延长线于点E,
∵菱形的面积为:15cm2,BC=5cm,
∴AE=3cm,则BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=4(cm),
∴EC=4+5=9(cm),
如图2,同理可得:AE=3cm,BE=4cm,
则EC=5-4=1(cm).
故答案为:1cm或9cm.
点评 此题主要考查了菱形的性质以及勾股定理,根据题意得出菱形的周长和面积是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
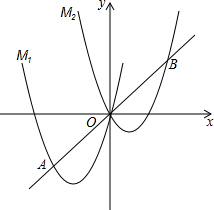 如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1
如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
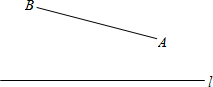 在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.
在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
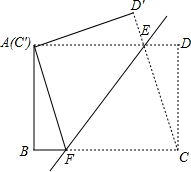 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com