
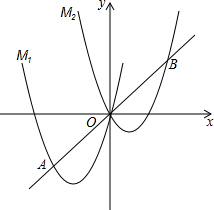
 Èçͼ£¬½«Å×ÎïÏßM1£ºy1=ax2+4xỊ̈Ó̉ƽ̉Æ3¸öµ¥Î»£¬ÔÙỊ̈ÉÏƽ̉Æ3¸öµ¥Î»£¬µĂµ½Å×ÎïÏßy2£¬¼ÇΪM2£¬Ö±Ïßy=xÓëM1
Èçͼ£¬½«Å×ÎïÏßM1£ºy1=ax2+4xỊ̈Ó̉ƽ̉Æ3¸öµ¥Î»£¬ÔÙỊ̈ÉÏƽ̉Æ3¸öµ¥Î»£¬µĂµ½Å×ÎïÏßy2£¬¼ÇΪM2£¬Ö±Ïßy=xÓëM1·ÖÎö £¨1£©¢Ù½«µăAºá×ø±ê´úÈëy=x£¬¼´¿ÉµĂ³öµăA×Ư×ø±ê£¬´Ó¶øµĂ³öµăAµÄ×ø±ê£¬¸ù¾ƯµăAÔÚÅ×ÎïÏßM1£ºy=ax2+4xÉÏ£¬´úÈë¼´¿ÉµĂ³öaµÄÖµ£¬½«Å×ÎïÏßM1»¯Îª¶¥µăʽ£¬¸ù¾Ưƽ̉ƵÄÔỘ¼´¿ÉµĂ³öÅ×ÎïÏßM2£»
¢Ú½«y=x´úÈëM2µÄ±í´ïʽ£¬¼´¿ÉµăBµÄ×ø±ê£»
£¨2£©¢Ù°ÑµăCºá×ø±ê´úÈëy=x£¬¼´¿ÉµĂ³öµăC×ø±ê£¬´Ó¶øµĂ³öµăF×ø±ê£¬°ÑµăF´úÈëy=x+n¼´¿ÉµĂ³önµÄÖµ£»
¢Ú¸ù¾ƯÖ±Ïßy=x+nÓëƠư·½ĐÎCDEFʼÖƠĂ»ÓĐ¹«¹²µă£¬Ö±½Ó¿ÉµĂ³önµÄÈ¡Öµ·¶Î§£»
£¨3£©Å×ÎïÏßM3Óë¡÷OBHµÄ±ß½ç×ÜÓĐÁ½¸ö¹«¹²µă£¬¼´Å×ÎïÏßÓëÏ߶ÎOBÓĐ2¸ö½»µăʱ£¬kµÄÈ¡Öµ·¶Î§£®
½â´đ ½â£º£¨1£©¢Ù¡ßµăAÔÚÖ±Ïßy=x£¬Ç̉µăAµÄºá×ø±êÊÇ-3£¬
¡àA£¨-3£¬-3£©£¬
°ÑA£¨-3£¬-3£©´úÈëy=ax2+4x£¬
½âµĂa=1£®
¡àM1£ºy=x2+4x£¬¶¥µăΪ£¨-2£¬-4£©£®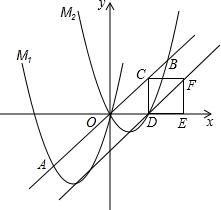 ¡àM2µÄ¶¥µăΪ£¨1£¬-1£©£¬
¡àM2µÄ¶¥µăΪ£¨1£¬-1£©£¬
¡àM2µÄ±í´ïʽΪy=x2-2x£»
¢Ú½«y=x´úÈëy=x2-2x£¬µĂx=x2-2x£¬
½âµĂx1=3£¬x2=0£¨ÉáÈ¥£©£¬
¡àµăBµÄ×ø±êΪ£¨3£¬3£©£»
£¨2£©¢ÙÓÉ̀ẩ⣬C£¨2£¬2£©£¬
¡àF£¨4£¬2£©£®
¡ßÖ±Ïßy=x+n¾¹ưµăF£¬
¡à2=4+n£¬
½âµĂn=-2£»
¢ÚÓÉ̀ẩâµĂ£ºnµÄÈ¡Öµ·¶Î§ÊÇn£¾3£¬n£¼-6£»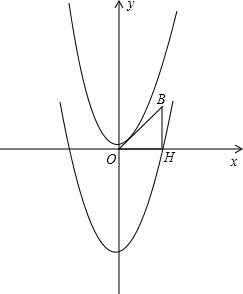 £¨3£©ÓÉ̀ẩ⣬Å×ÎïÏßM3µÄ½âÎöʽΪy=x2+k£®
£¨3£©ÓÉ̀ẩ⣬Å×ÎïÏßM3µÄ½âÎöʽΪy=x2+k£®
µ±Å×ÎïÏß¾¹ưµăH£¨3£¬0£©Ê±£¬32+k=0£¬
½âµĂk=-9£®
¡ßO£¨0£¬0£©£¬B£¨3£¬3£©£¬
¡àÖ±ÏßOBµÄ½âÎöʽΪy=x£®
ÓÉ$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}+k}\end{array}\right.$£¬
µĂx2-x+k=0£¬¢Ù
µ±¡÷=£¨-1£©2-4¡Á1¡Ák=0£¬¼´k=$\frac{1}{4}$ʱ£¬Å×ÎïÏßM3ÓëÖ±ÏßOBÖ»ÓĐ̉»¸ö¹«¹²µă£¬
´Ëʱ·½³̀¢Ù»¯Îªx2-x+$\frac{1}{4}$=0£¬
½âµĂx=$\frac{1}{2}$£¬
¼´¹«¹²µăµÄºá×ø±êΪ$\frac{1}{2}$£¬´Ëʱ¹«¹²µăÔÚÏ߶ÎOBÉÏ£®
¡àkµÄÈ¡Öµ·¶Î§ÊÇ-9£¼k£¼$\frac{1}{4}$£®
µăÆÀ ±¾̀âÊǶ₫´Îº¯ÊưµÄ×ÛºÏ̀⣬Éæ¼°µÄ֪ʶµă£ºÓĂ´ư¶¨ÏµÊư·¨Çóº¯Êư½âÎöʽ£¬Ơư·½ĐεÄĐÔÖÊ£¬Á½º¯Êư½»µă×ø±êµÄÇ󷨣¬¶₫´Îº¯ÊưͼÏóÓ뼸ºÎ±ä»»£¬ÀûÓĂ·½³̀˼ÏëÓëÊưĐνáºÏÊǽầâµÄ¹Ø¼ü£®


 ÖÇȤº®¼Ù×÷̉µÔÆÄϿƼ¼³ö°æÉçϵÁĐ´đ°¸
ÖÇȤº®¼Ù×÷̉µÔÆÄϿƼ¼³ö°æÉçϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | Èñ½Ç | B£® | Ö±½Ç | C£® | ¶Û½Ç | D£® | Î̃·¨È·¶¨ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | ¶₫¸ö½»µă | B£® | ̉»¸ö½»µă | C£® | Î̃½»µă | D£® | ²»ÄÜÈ·¶¨ |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com