
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=0①}\\{2x+y=6②}\end{array}\right.$,
①+②得:3x=6,即x=2,
把x=2代入①得:y=2,
则方程组的解为$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-5y=-17①}\\{3x+4y=32②}\end{array}\right.$,
①×4+②×5得:23x=92,即x=4,
把x=4代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}x=4\\ y=5\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:解答题
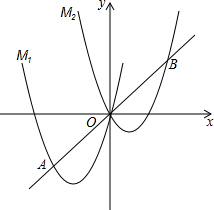 如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1
如图,将抛物线M1:y1=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线y2,记为M2,直线y=x与M1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
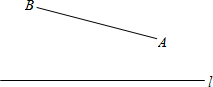 在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.
在一个平面河岸l同侧有A、B两个村庄,A、B到l的距离分别为3km和2km,AB=xkm(x>1),现计划在河岸l上建抽水站P,用输水管道向两个村庄供水.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
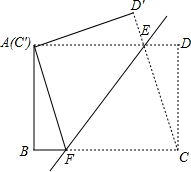 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
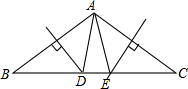 如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )
如图,△ABC中,AB、AC的垂直平分线分别交BC于D、E,且∠DAE=20°,则∠BAC=( )| A. | 100° | B. | 120° | C. | 150° | D. | 160° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
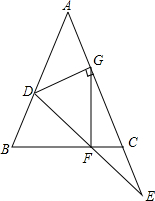 如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.
如图,在△ABC中,AB=AC,D是AB上一点,点E在AC的延长线上,且BD=CE,连结DE交BC于F,过点D作DG⊥AE,垂足为G,连结FG.若FG=$\sqrt{2}$,∠E=30°,则GE=$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
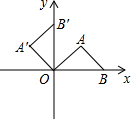 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )| A. | (1,1) | B. | (-1,1) | C. | (1,-1) | D. | $(-\sqrt{2},\sqrt{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com