练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在圆⊙O内有折线OABC，其中OA=8，AB=12，∠A=∠B=60°，则BC的长为（　　）

    A. 19 B. 16 C. 18 D. 20

    【答案】D

    【解析】试题分析：延长AO交BC于D，根据∠A、∠B的度数易证得△ABD是等边三角形，由此可求出OD、BD的长；过O作BC的垂线，设垂足为E；在Rt△ODE中，根据OD的长及∠ODE的度数易求得DE的长，进而可求出BE的长；由垂径定理知BC=2BE，由此得解．

    延长AO交BC于D，作OE⊥BC于E；

    ∵∠A=∠B=60°，

    ∴∠ADB=60°；

    ∴△ADB为等边三角形；

    ∴BD=AD=AB=12；

    ∴OD=4，

    又∵∠ADB=60°，

    ∴DE=OD=2；

    ∴BE=10；

    ∴BC=2BE=20；

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某花圃销售一批名贵花卉，平均每天可售出20盆，每盆盈利40元，为了增加盈利并尽快减少库存，花圃决定采取适当的降价措施，经调查发现，如果每盆花卉每降1元，花圃平均每天可多售出2盆．

    （1）若花圃平均每天要盈利1200元，每盆花卉应降价多少元？

    （2）每盆花卉降低多少元时，花圃平均每天盈利最多，是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB与CD相交于点O，且∠OAD=∠OCB，延长AD、CB交于点P，那么图中的相似三角形的对数为______ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F.

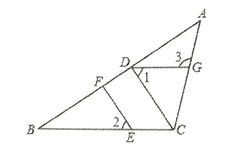
    (1) CD与EF平行吗？为什么？

    (2)如果∠1=∠2，且∠3=115°，求∠ACB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现：如图 1，已知点 F，G 分别在直线 AB，CD 上，且 AB∥CD，若∠BFE=40°，∠CGE=130°，则∠GEF 的度数为 ；

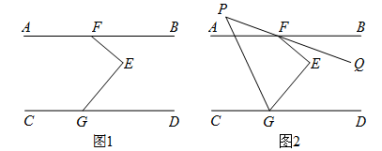
    （2）拓展探究：∠GEF，∠BFE，∠CGE 之间有怎样的数量关系？写出结论并给出证明； 答：∠GEF= .

    证明：过点 E 作 EH∥AB，

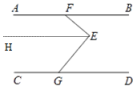
    ∴∠FEH=∠BFE（ ），

    ∵AB∥CD，EH∥AB，（辅助线的作法）

    ∴EH∥CD（ ），

    ∴∠HEG=180°-∠CGE（ ），

    ∴∠FEG=∠HFG+∠FEH= .

    （3）深入探究：如图 2，∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P，试探究∠GPQ 与∠GEF 之间的数量关系，请直接写出你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=ax+b的图象经过点A(1,3)且与y=2x-3 平行．

    (1)求出a,b.写出y 与x 的函数关系；

    (2)求当x=-2 时，y的值，当y=10 时，x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，高AD和BE所在的直线交于点H，且BH＝AC，则∠ABC等于(　)

    A. 45° B. 120° C. 45°或135° D. 45°或120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下面三行数：

    （1）第①行数按什么规律排列？

    （2）第②③行数与第①行数分别有什么关系；

    （3）设分别为第①②③行的2012个数，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一段长为250km的高速公路需要维修，现由甲、乙两个工程队先后接力完成，共用时15天，已知甲工程队每天维修20km，乙工程队每天维修15km．求甲、乙两个工程队分别维修了多长的高速公路？（用一元一次方程解决问题）

    查看答案和解析>>

    同步练习册答案