
【题目】(1)问题发现:如图 1,已知点 F,G 分别在直线 AB,CD 上,且 AB∥CD,若∠BFE=40°,∠CGE=130°,则∠GEF 的度数为 ;
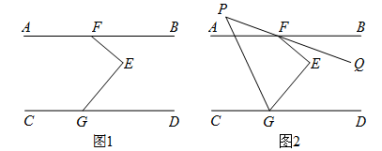
(2)拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明; 答:∠GEF= .
证明:过点 E 作 EH∥AB,
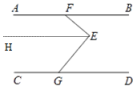
∴∠FEH=∠BFE( ),
∵AB∥CD,EH∥AB,(辅助线的作法)
∴EH∥CD( ),
∴∠HEG=180°-∠CGE( ),
∴∠FEG=∠HFG+∠FEH= .
(3)深入探究:如图 2,∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P,试探究∠GPQ 与∠GEF 之间的数量关系,请直接写出你的结论.
【答案】(1)90°(2)∠BFE+180°∠CGE;两直线平行,内错角相等;平行线的迁移性;两直线平行,同旁内角互补;∠BFE+180°∠CGE(3)∠GPQ+![]() ∠GEF=90°
∠GEF=90°
【解析】
(1)如图1,过E作EH∥AB,根据平行线的性质可得∠HEF=∠BFE=40![]() ,∠HEG=50
,∠HEG=50![]() ,相加可得结论;
,相加可得结论;
(2)由①知:∠HEF=∠BFE,∠HEG+∠CGE=180°,则∠HEG=180°∠CGE,两式相加可得∠GEF=∠BFE+180°∠CGE;
(3)如图2,根据角平分线的定义得:∠BFQ=![]() ∠BFE,∠CGP=
∠BFE,∠CGP=![]() ∠CGE,由三角形的外角的性质得:∠GPQ=∠GMF∠PFM=∠CGP∠BFQ,计算∠GPQ+
∠CGE,由三角形的外角的性质得:∠GPQ=∠GMF∠PFM=∠CGP∠BFQ,计算∠GPQ+![]() ∠GEF并结合②的结论可得结果.
∠GEF并结合②的结论可得结果.
(1)如图1,过E作EH∥AB,

∵AB∥CD,
∴AB∥CD∥EH,
∴∠HEF=∠BFE=40°,∠HEG+∠CGE=180°,
∵∠CGE=130°,
∴∠HEG=50°,
∴∠GEF=∠HEF+∠HEG=40°+50°=90°;
故答案为:90°;
(2)∠GEF=∠BFE+180°∠CGE,
证明:过点 E 作 EH∥AB,

∴∠FEH=∠BFE(两直线平行,内错角相等),
∵AB∥CD,EH∥AB,(辅助线的作法)
∴EH∥CD(平行线的迁移性),
∴∠HEG=180°-∠CGE(两直线平行,同旁内角互补),
∴∠FEG=∠HFG+∠FEH=∠BFE+180°∠CGE,
故答案为:∠BFE+180°∠CGE;两直线平行,内错角相等;平行线的迁移性;两直线平行,同旁内角互补;∠BFE+180°∠CGE;
(3)∠GPQ+![]() ∠GEF=90°,
∠GEF=90°,
理由是:如图2,∵FQ平分∠BFE,GP平分∠CGE,

∴∠BFQ=![]() ∠BFE,∠CGP=
∠BFE,∠CGP=![]() ∠CGE,
∠CGE,
在△PMF中,∠GPQ=∠GMF∠PFM=∠CGP∠BFQ,
∴∠GPQ+![]() ∠GEF=
∠GEF=![]() ∠CGE
∠CGE![]() ∠BFE+
∠BFE+![]() ∠GEF=
∠GEF=![]() ×180°=90°.
×180°=90°.
即∠GPQ+![]() ∠GEF=90°.
∠GEF=90°.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,……,则第⑩个图形中棋子的颗数为__________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是直角三角形ABC斜边AB上一点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.

(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ;
(2)如图2,当点P在线段AB上不与点Q重合时,若AC=BC,CE:AE=1:3,△FBQ的面积等于3,求△AQE的面积;
(3)如图3,当点P在线段BA的延长线上时,请画出符合条件的图形.若AC=BC,AE:CE=1:3,△FEQ的面积等于3,求△AQE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB边的垂直平分线l1交BC于D,AC边的垂直平分线l2交BC于E,l1与l2相交于点O.△ADE的周长为6cm.

(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在圆⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )

A. 19 B. 16 C. 18 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠BAC=∠EAD=90o.
(1)判断∠BAE与∠CAD的大小关系,并说明理由.
(2)当∠EAC=60o时,求∠BAD的大小.
(3)探究∠EAC与∠BAD的数量关系,请直接写出结果,不要求说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0
②a﹣b+c<0
③阴影部分的面积为4
④若c=﹣1,则b2=4a.

查看答案和解析>>
科目:初中数学 来源: 题型:
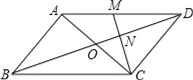
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com