
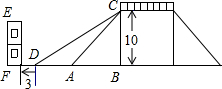
 如图是成都市某街道的一座人行天桥的示意图,天桥的高是10米,坡面AC的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度,使新坡面DC的倾斜角为30°,若新坡脚前需留3米的人行道,问高原坡脚10米的建筑物EF是否需要拆除?请说明理由.(参考数据:$\sqrt{3}≈1.732$,$\sqrt{2}≈1.414$.)
如图是成都市某街道的一座人行天桥的示意图,天桥的高是10米,坡面AC的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度,使新坡面DC的倾斜角为30°,若新坡脚前需留3米的人行道,问高原坡脚10米的建筑物EF是否需要拆除?请说明理由.(参考数据:$\sqrt{3}≈1.732$,$\sqrt{2}≈1.414$.) 分析 由已知天桥的高是10米,坡面的倾斜角为45°,易求得AB的长;又由新坡面的倾斜角为30°,根据坡角的定义,可求得BD的长,从而求得AD的长,然后将AD+3与10进行比较,若大于则需拆除,反之不用拆除.
解答 解:根据题意得:∠CAB=45°,BC=10米,
∴AB=BC=10米,
∵新坡面DC的倾斜角为30°,
∴tan∠CDB=$\frac{BC}{BD}$=$\frac{\sqrt{3}}{3}$,
∴BD=10$\sqrt{3}$米,
∴AD=10$\sqrt{3}$-10≈7.32(米),
∵7.32+3>10.
∴离原坡角10米的建筑物需要拆除.
点评 此题主要考查解直角三角形的应用,解答此题的关键是掌握坡度与坡角的定义,此题难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com