
【题目】阅读并填空完善下列证明过程:
如图,已知BC⊥AC于C,DF⊥AC于D,∠1+∠2=180°,
求证:∠GFB=∠DEF﹒
证明:∵BC⊥AC于C,DF⊥AC于D(已知),
∴∠C=∠ =90°( ),
∴CB∥FD(同位角相等,两直线平行),
∴∠1+∠3=180°( )
又∵∠1+∠2=180°(已知),
∴∠2=∠3( ),
∴ ∥ ( ),
∴∠GFB=∠DEF( )

【答案】ADF;垂直的定义;两直线平行,同旁内角互补;同角的补角相等;DE;FG;内错角相等,两直线平行;两直线平行,同位角相等.
【解析】
首先根据![]() ,
,![]() 可以得到
可以得到![]() ,这是利用垂直的定义;其次由
,这是利用垂直的定义;其次由![]() 得到
得到![]() ,这是根据同位角相等,两直线平行;紧接着由
,这是根据同位角相等,两直线平行;紧接着由![]() 得到
得到![]() ,这是根据两直线平行,同旁内角互补;而已知条件中有
,这是根据两直线平行,同旁内角互补;而已知条件中有![]() ,所以利用同角的补角相等得到
,所以利用同角的补角相等得到![]() ,所以
,所以![]() ,这是根据内错角相等,两直线平行;由
,这是根据内错角相等,两直线平行;由![]() 便可以得到
便可以得到![]() ,这是根据两直线平行,同位角相等;
,这是根据两直线平行,同位角相等;
∵![]() 于
于![]() ,
,![]() 于
于![]() (已知),
(已知),
∴![]() (垂直的定义),
(垂直的定义),
∴![]() (同位角相等,两直线平行 ),
(同位角相等,两直线平行 ),
∴![]() (两直线平行,同旁内角互补)
(两直线平行,同旁内角互补)
又∵![]() (已知),
(已知),
∴![]() (同角的补角相等),
(同角的补角相等),
∴![]() (内错角相等,两直线平行),
(内错角相等,两直线平行),
∴![]() (两直线平行,同位角相等).
(两直线平行,同位角相等).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
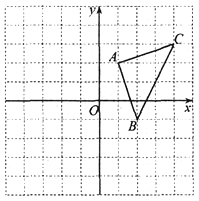
【题目】如图,平面直角坐标系中,△ABC的顶点坐标为:A(1,2),B(2, 一1), C (4, 3).
(1)将△ABC向左平移2个单位长度,再向上平移1个单位长度,得△A'B'C'.画出△A'B'C',并写出△A'B'C'的顶点坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=30 cm,BC=35 cm,∠B=60°,有一动点M自A向B以1 cm/s的速度运动,动点N自B向C以2 cm/s的速度运动,若M,N同时分别从A,B出发.
(1)经过多少秒,△BMN为等边三角形;
(2)经过多少秒,△BMN为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
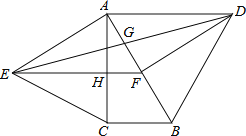
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F, 
(1)求证:△ABF≌△ECF;
(2)若AE=AD,连接AC、BE,求证:四边形ABEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一,现有足够多的边长为![]() 的小正方形纸片(
的小正方形纸片(![]() 类)、长为
类)、长为![]() 宽为
宽为![]() 的长方形纸片(
的长方形纸片(![]() 类)以及边长为
类)以及边长为![]() 的大正方形纸片(
的大正方形纸片(![]() 类).
类).
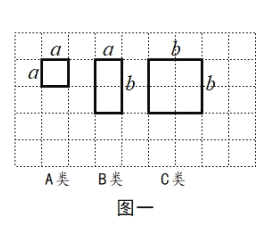
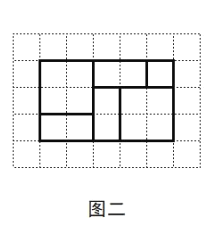
如图二,小明利用上述三种纸片各若干张,拼出了一个长为![]() ,宽为
,宽为![]() 的长方形,并用这个长方形解释了等式
的长方形,并用这个长方形解释了等式![]()
![]() 是成立的.
是成立的.
(1)若取图一中的纸片若干张(三种都要取到)拼成一个长方形(所取纸片用完无剩余),使它的长和宽分别为![]() ,请你通过计算说明需要
,请你通过计算说明需要![]() 类卡片多少张;
类卡片多少张;
(2)若取![]() 类纸片
类纸片![]() 张,
张,![]() 类纸片
类纸片![]() 张,
张,![]() 类纸片
类纸片![]() 张,能拼成一个长方形吗(所取纸片用完无剩余)?请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式;
张,能拼成一个长方形吗(所取纸片用完无剩余)?请你在图三中画出示意图并在下面直接写出能用该长方形来解释成立的等式;


(3)如图四,大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]() ,用四个完全相同的长方形的长和宽为别为
,用四个完全相同的长方形的长和宽为别为![]()
![]() .请你通过观察或计算,判断下列
.请你通过观察或计算,判断下列![]() 个式子是否成立,将其中成立的式子的都填写在横线上: (直接填写序号).
个式子是否成立,将其中成立的式子的都填写在横线上: (直接填写序号).
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )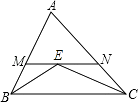
A.12
B.4
C.8
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com