
【题目】如图,已知∠AOB=∠BOC=∠COD,下列结论中错误的是( )

A. OB、OC分别平分![]() 、
、![]()
B. ![]()
C. ![]()
D. ![]()
科目:初中数学 来源: 题型:
【题目】吉林省广播电视塔(简称“吉塔”)是我省目前最高的人工建筑,也是俯瞰长春市美景的最佳去处.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度.已知如图将无人机置于距离“吉塔”水平距离138米的点C处,则从无人机上观测塔尖的仰角恰为30°,观测塔基座中心点的俯角恰为45°.求“吉塔”的高度.(注: ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)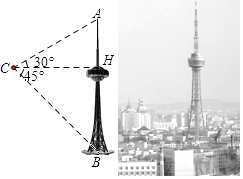
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并填空完善下列证明过程:
如图,已知BC⊥AC于C,DF⊥AC于D,∠1+∠2=180°,
求证:∠GFB=∠DEF﹒
证明:∵BC⊥AC于C,DF⊥AC于D(已知),
∴∠C=∠ =90°( ),
∴CB∥FD(同位角相等,两直线平行),
∴∠1+∠3=180°( )
又∵∠1+∠2=180°(已知),
∴∠2=∠3( ),
∴ ∥ ( ),
∴∠GFB=∠DEF( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
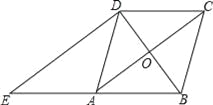
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为![]() .现有格点
.现有格点![]() ,那么,在网格图中找出格点
,那么,在网格图中找出格点![]() ,使以
,使以![]() 和格点
和格点![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() .这样的
.这样的![]() 点可找到的个数为( )
点可找到的个数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地治理水质,保护环境,某污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少8万元.
(1)A、B两种型号的设备每台的价格是多少?
(2)若污水处理公司购买设备的预算资金不超过125万元,你认为该公司有哪几种购买方案?
(3)若每月需处理的污水约2040m3,在不突破(2)中资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣3,3),B(﹣1,1.5),将线段AB向右平移d个单位长度后,点A、B恰好同时落在反比例函数y= ![]() (x>0)的图象上,则d等于( )
(x>0)的图象上,则d等于( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:
对于两个不等的非零实数a、b,若分式![]() 的值为零,则x=a或x=b.又因为
的值为零,则x=a或x=b.又因为![]() =
=![]() ,所以关于x的方程x+
,所以关于x的方程x+![]() =a+b有两个解,分别为x1=a,x2=b.
=a+b有两个解,分别为x1=a,x2=b.
应用上面的结论解答下列问题:
(1)方程x+![]() =q的两个解分别为x1=﹣1、x2=4,则P= ,q= ;
=q的两个解分别为x1=﹣1、x2=4,则P= ,q= ;
(2)方程x+![]() =4的两个解中较大的一个为 ;
=4的两个解中较大的一个为 ;
(3)关于x的方程2x+![]() =2n的两个解分别为x1、x2(x1<x2),求
=2n的两个解分别为x1、x2(x1<x2),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com