
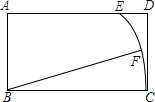
 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$. 分析 连接CE交BF于H,连接BE,根据矩形的性质求出AB=CD=3,AD=BC=5=BE,∠A=∠D=90°,根据勾股定理求出AE=4,求出DE=1,根据勾股定理求出CE,求出CH,解直角三角形求出即可.
解答 解:连接CE交BF于H,连接BE,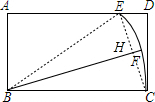
∵四边形ABCD是矩形,AB=3,BC=5,
∴AB=CD=3,AD=BC=5=BE,∠A=∠D=90°,
由勾股定理得:AE=$\sqrt{{5}^{2}-{3}^{2}}$=4,DE=5-4=1,
由勾股定理得:CE=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
由垂径定理得:CH=EH=$\frac{1}{2}$CE=$\frac{\sqrt{10}}{2}$,
在Rt△BHC中,由勾股定理得:BH=$\sqrt{{5}^{2}-(\frac{\sqrt{10}}{2})^{2}}$=$\frac{3\sqrt{10}}{2}$,
所以tan∠FBC=$\frac{FC}{BH}$=$\frac{\frac{\sqrt{10}}{2}}{\frac{3\sqrt{10}}{2}}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了矩形的性质,勾股定理,解直角三角形,垂径定理的应用,能正确作出辅助线并构造出直角三角形是解此题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
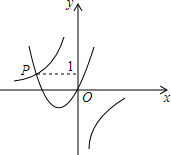 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解是x=-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
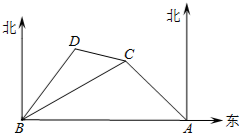 2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.
2016年1月6日,我国南沙永暑礁新建港口、机场完成试航试飞,将为岛礁物资运输、人员往来、通信导航、救援补给提供便捷支持,使航行和飞行更为安全可靠.如图所示,永暑礁新建港口在A处,位于港口A的正西方的有一小岛B,小岛C在小岛B的北偏东60°方向,小岛C在A的北偏西45°方向;小岛D在小岛B的北偏东38°方向且满足∠BCD=37°,港口A和小岛C的距离是23$\sqrt{2}$km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年12月27当日上午8时42分,第一列“和谐号”动车驶入扬州火车站.已知动车的速度比普通客车的速度快70km/h,小路同学从扬州去A地游玩,本打算乘坐普通客车,需要2小时才能到达;由于得知开通了动车,决定乘坐动车,她发现乘坐动车比乘坐普通客车节约40分钟.求动车的速度和扬州与A地之间的距离.
2015年12月27当日上午8时42分,第一列“和谐号”动车驶入扬州火车站.已知动车的速度比普通客车的速度快70km/h,小路同学从扬州去A地游玩,本打算乘坐普通客车,需要2小时才能到达;由于得知开通了动车,决定乘坐动车,她发现乘坐动车比乘坐普通客车节约40分钟.求动车的速度和扬州与A地之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )
如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发,以同样的速度沿边BC、DC向点C运动.下列四个结论:①AE=AF;②∠CEF=∠CFE;③当E、F分别是边BC、DC的中点时,EF=$\sqrt{3}$BE;④当E、F分别是边BC、DC的中点时,△AEF的面积最大,其中,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com