
 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以时为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.分析 (1)过P点作PM⊥BC,垂足为M,则PM=AB=$\sqrt{3}$.由等边三角形的性质得出∠PEF=60°,由三角函数求出PE即可;
(2)由矩形的性质证出 AD∥BC,得出∠PAH=∠FCH,再由对顶角相等即可得出结论;
(3)由等边三角形的性质得出EM═$\frac{1}{2}$EF=1,再由三角函数求出∠ACB=30°,由三角形的外角性质得出∠PAH=∠PHA,得出PH=AP,由矩形的性质得出AP=BM,即可得出结论.
解答 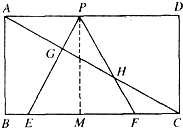 解:(1)过P点作PM⊥BC,垂足为M,如图所示:
解:(1)过P点作PM⊥BC,垂足为M,如图所示:
则PM=AB=$\sqrt{3}$.
∵△PEF为等边三角形,
∴∠PEF=60°.
在Rt△PEM中,PE=$\frac{PM}{sin60°}$=2,
∴△PEF的边长为2.
(2)△AHP∽△CHF,理由如下:
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠PAH=∠FCH.
又∵∠AHP=∠CHF,
∴△AHP∽△CHF.
(3)在等边△PEF中,PM⊥BC,
则四边形ABMP为矩形;
由三线合一得:EM=$\frac{1}{2}$EF=1.
在Rt△ABC中,tan∠ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,
∴∠ACB=30°.
又∵△FHC的外角∠BFH=60°,
∴∠FCH=∠FHC=30°,
则∠PAH=∠PHA,
∴PH=AP.
∵四边形ABMP为矩形,
∴AP=BM,
∴AP=BM=BE+EM=BE+1.
即y=x+1,其中0≤x≤1.
点评 本题是四边形综合题目,考查了矩形的性质与判定、等边三角形的性质、三角函数、相似三角形的判定与性质、三角形的外角性质等知识;本题难度较大,综合性强,利于培养学生的创新能力.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,2) | B. | (-3,-2) | C. | (2,-2) | D. | (-1,6) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
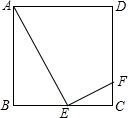 如图,正方形ABCD的边长为1,动点E在BC上,∠AEF=90°,EF交DC于F,当线段FC最长时,BE的长为$\frac{1}{2}$.
如图,正方形ABCD的边长为1,动点E在BC上,∠AEF=90°,EF交DC于F,当线段FC最长时,BE的长为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
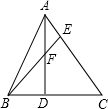 如图,△ABC中,D、E是BC、AC上的点,AD、BE交于F,若已知BD:DC=2:3,AE:EC=1:3.
如图,△ABC中,D、E是BC、AC上的点,AD、BE交于F,若已知BD:DC=2:3,AE:EC=1:3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com