
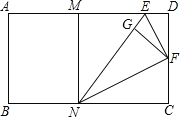
【题目】如图,矩形ABCD,![]() ,
,![]() ,点M,N分别为边AD和边BC上的两点,且
,点M,N分别为边AD和边BC上的两点,且![]() ,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将
,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将![]() 沿着EF所在的直线折叠,将
沿着EF所在的直线折叠,将![]() 沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点
沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点![]() 以下结论中:
以下结论中:
![]() ;
;![]() ;
;![]() ∽
∽![]() ;
;![]() 四边形MNCD是正方形;
四边形MNCD是正方形;![]() 其中正确的结论是
其中正确的结论是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
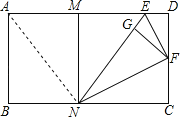
由折叠的性质得到∠DFE=∠GFE,∠GFN=∠CFN,根据平角的定义得到EF⊥NF;故①正确;连接AN,根据轴对称的性质得到∠ANM=∠ENM,推出∠MNE≠∠CNE;故②错误;根据余角的性质得到∠DFE≠∠NEM,推出△MNE∽△DEF错误,故③错误;设DE=x,根据相似三角形的性质得到CN=8,推出四边形MNCD是正方形;故④正确;根据线段的和差得到AM=6,故⑤错误.
∵由折叠的性质得,∠DFE=∠GFE,∠GFN=∠CFN,
∵∠DFE+∠GFE+∠GFN+∠CFN=180°,
∴∠GFN+∠CFN=90°,
∴∠NFE=90°,
∴EF⊥NF;故①正确;
连接AN,
∵点E是点A关于MN所在的直线的对称点,
∴∠ANM=∠ENM,
∴∠ANB=∠CNE,
而四边形ABNM不是正方形,
∴∠ANB≠∠ANM,
∴∠MNE≠∠CNE;故②错误;
∵∠NEF≠90°,∠DFE+∠DEF=90°,∠DEF+∠MEN≠90°,
∴∠DFE≠∠NEM,
∴△MNE∽△DEF错误,故③错误;
设DE=x,
∴BN=AM=![]() ,
,
∴CN=14﹣BN=![]() ,
,
∵∠EFD+∠CFN=∠EFD+∠DEF=90°,
∴∠DEF=∠CFN,
∵∠D=∠C=90°,
∴△DEF∽△CFN,
∴![]() ,
,
∵F是CD的在中点,
∴CF=DF=4,
∴![]() ,
,
∴x=2,x=﹣16(不合题意舍去),
∴DE=2,CN=8,
∴CD=CN,
∴四边形MNCD是正方形;故④正确;
∵CN=DM=8,
∴AM=6,故⑤错误,
故选:B.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
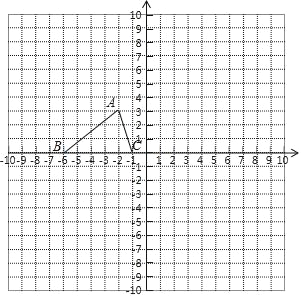
【题目】如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点P的坐标 .
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点Q的坐标 .
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
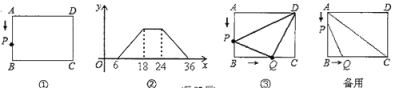
【题目】如图①,在矩形![]() 中,动点
中,动点![]() 从
从![]() 出发,以相同的速度,沿
出发,以相同的速度,沿![]() 方向运动到点
方向运动到点![]() 处停止.设点
处停止.设点![]() 运动的路程为
运动的路程为![]() ,
, ![]() 面积为
面积为![]() ,
,![]() 与
与![]() 的函数图象如图②所示.
的函数图象如图②所示.
(1)矩形![]() 的面积为 ;
的面积为 ;
(2)如图③,若点![]() 沿
沿![]() 边向点
边向点![]() 以每秒1个单位的速度移动,同时,点
以每秒1个单位的速度移动,同时,点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以每秒2个单位的速度移动.如果
以每秒2个单位的速度移动.如果![]() 、
、![]() 两点在分别到达
两点在分别到达![]() 、
、![]() 两点后就停止移动,回答下列问题:
两点后就停止移动,回答下列问题:
①当运动开始![]() 秒时,试判断
秒时,试判断![]() 的形状;
的形状;
②在运动过程中,是否存在这样的时刻,使以![]() 为圆心,
为圆心,![]() 的长为半径的圆与矩形
的长为半径的圆与矩形![]() 的对角线
的对角线![]() 相切,若存在,求出运动时间;若不存在,请说明理由.
相切,若存在,求出运动时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
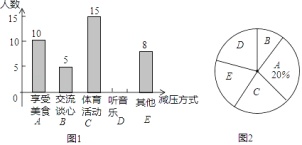
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
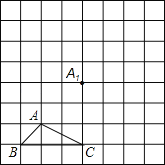
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
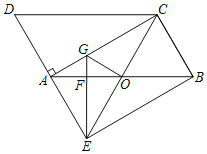
【题目】如图,在平行四边形ABCD中,![]() ,延长DA于点E,使得
,延长DA于点E,使得![]() ,连接BE.
,连接BE.
![]() 求证:四边形AEBC是矩形;
求证:四边形AEBC是矩形;
![]() 过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若
过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
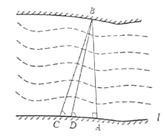
【题目】如图,一座大桥的两端位于河的 A、B 两点,某同学为了测量 A、B 两点之间的河宽,在垂直于大桥 AB 的直线型道路 l 上测得了如下的数据:∠BDA=76.1°,∠BCA=68.2°,CD=42.8 米。求大桥 AB 的长(精确到 1 米) 参考数据:sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0,sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
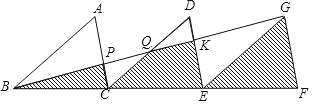
【题目】如图,已知△ABC≌△DCE≌△GEF,三条对应边BC.CE、EF在同一条直线上,连接BG,分别交AC、DC、DE于点P、Q、K,其中S△PQC=3,则图中三个阴影部分的面积和为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com