
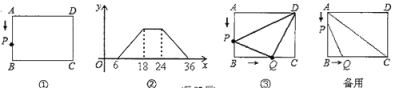
【题目】如图①,在矩形![]() 中,动点
中,动点![]() 从
从![]() 出发,以相同的速度,沿
出发,以相同的速度,沿![]() 方向运动到点
方向运动到点![]() 处停止.设点
处停止.设点![]() 运动的路程为
运动的路程为![]() ,
, ![]() 面积为
面积为![]() ,
,![]() 与
与![]() 的函数图象如图②所示.
的函数图象如图②所示.
(1)矩形![]() 的面积为 ;
的面积为 ;
(2)如图③,若点![]() 沿
沿![]() 边向点
边向点![]() 以每秒1个单位的速度移动,同时,点
以每秒1个单位的速度移动,同时,点![]() 从点
从点![]() 出发沿
出发沿![]() 边向点
边向点![]() 以每秒2个单位的速度移动.如果
以每秒2个单位的速度移动.如果![]() 、
、![]() 两点在分别到达
两点在分别到达![]() 、
、![]() 两点后就停止移动,回答下列问题:
两点后就停止移动,回答下列问题:
①当运动开始![]() 秒时,试判断
秒时,试判断![]() 的形状;
的形状;
②在运动过程中,是否存在这样的时刻,使以![]() 为圆心,
为圆心,![]() 的长为半径的圆与矩形
的长为半径的圆与矩形![]() 的对角线
的对角线![]() 相切,若存在,求出运动时间;若不存在,请说明理由.
相切,若存在,求出运动时间;若不存在,请说明理由.
【答案】(1)72;(2)①![]() 为直角三角形;②不存在
为直角三角形;②不存在
【解析】
(1)通过图形可以求出矩形的长和宽,然后计算矩形的面积;
(2)①通过速度,可计算出PD、PQ、DQ的长,然后建立勾股定理,可得△PDQ为直角三角形;
②过Q作QM⊥AC,通过计算QM和PQ的长,利用两条线段长度相等,可列出方程,计算方程的解就是运动时间;若方程无解,则情况不成立.
解:(1)由图象②可得长方形的长和宽为12和6,则面积为:12×6=72;
(2)①由题意可知:AP=![]() ,BP=
,BP=![]() ,BQ=3,CQ=9
,BQ=3,CQ=9
∴在Rt△APD中:![]()
在Rt△BPQ中:![]()
在Rt△CDQ中:![]()
∵![]() 即:
即:![]()
∴△DPQ为直角三角形
②不存在.理由:假设存在,连接AC,过点Q作QM垂直于AC垂足为点M.
则QM=PQ,即得:![]()
即![]()
化简得:![]()
∵△<0
∴此方程无解,即不存在


科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )
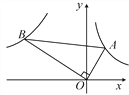
A. -3 B. -4 C. -![]() D. -2
D. -2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台电脑和打印机,如果购买![]() 台电脑和
台电脑和![]() 台打印机,一共花费
台打印机,一共花费![]() 元;如果购买
元;如果购买![]() 台电脑和
台电脑和![]() 台打印机,一共花费
台打印机,一共花费![]() 元;
元;
(1)求每台电脑和每台打印机的价格分别是多少元?
(2)如果学校购买电脑和打印机的预算费用不超过![]() 元,并且购买打印机的台数要比购买电脑的台数多
元,并且购买打印机的台数要比购买电脑的台数多![]() 台,那么该学校最多能购买多少台打印机?
台,那么该学校最多能购买多少台打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
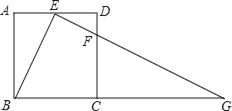
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
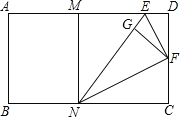
【题目】如图,矩形ABCD,![]() ,
,![]() ,点M,N分别为边AD和边BC上的两点,且
,点M,N分别为边AD和边BC上的两点,且![]() ,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将
,点E是点A关于MN所在的直线的对称点,取CD的中点F,连接EF,NF,分别将![]() 沿着EF所在的直线折叠,将
沿着EF所在的直线折叠,将![]() 沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点
沿着NF所在的直线折叠,点D和点C恰好重合于EN上的点![]() 以下结论中:
以下结论中:
![]() ;
;![]() ;
;![]() ∽
∽![]() ;
;![]() 四边形MNCD是正方形;
四边形MNCD是正方形;![]() 其中正确的结论是
其中正确的结论是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
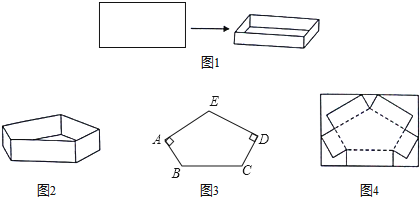
【题目】综合与实践:制作无盖盒子
任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为![]() 的无盖长方体盒子
的无盖长方体盒子![]() 纸板厚度忽略不计
纸板厚度忽略不计![]() .
.
![]() 请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.
![]() 请求出这块矩形纸板的长和宽.
请求出这块矩形纸板的长和宽.
任务二:图2是一个高为4cm的无盖的五棱柱盒子![]() 直棱柱
直棱柱![]() ,图3是其底面,在五边形ABCDE中,
,图3是其底面,在五边形ABCDE中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 试判断图3中AE与DE的数量关系,并加以证明.
试判断图3中AE与DE的数量关系,并加以证明.
![]() 图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果
图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果![]() 图中实线表示剪切线,虚线表示折痕
图中实线表示剪切线,虚线表示折痕![]() 纸板厚度及剪切接缝处损耗忽略不计
纸板厚度及剪切接缝处损耗忽略不计![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com