
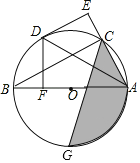
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D是![]() 的中点,DE是⊙O的切线,DF⊥AB于F,点G是
的中点,DE是⊙O的切线,DF⊥AB于F,点G是![]() 的中点
的中点
(1)求证:△ADE≌△ADF;
(2)若OF=3,AB=10,求图中阴影部分的面积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OD,证明DE∥BC,进而得∠E=∠DFA=∠ACB=90°,由D是![]() 的中点得∠DAE=∠DAF,再结合公共边,由AAS定理得结论;
的中点得∠DAE=∠DAF,再结合公共边,由AAS定理得结论;
(2)连接OD,OG,过O作OH⊥AC于H,过C作CK⊥OA于点K,由勾股定理求得 DF,便可得OH,再求AH,AK,再由相似三角形求得OM,最后求出扇形OAG,△OGM和△ACM的面积便可.
(1)证明:连接OD,如图1,

∵点D是![]() 的中点,
的中点,
∴∠DAF=∠DAE,OD⊥BC,
∵DE是⊙O的切线,
∴OD⊥DE,
∴DE∥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠AED=∠ACB=90°,
∵AD=AD,
∴:△ADE≌△ADF(AAS);
(2)连接OD,OG,过O作OH⊥AC于H,过C作CK⊥OA于点K,如图2,
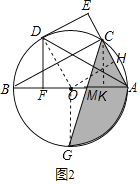
则AH=CH,∠GOA=∠GOB=90°,OA=OB=OD=5,
∴OH=DE=DF=![]() ,
,
∴CH=AH=![]() ,
,
∴BC=![]() ,
,
∵![]() ,
,
∴CK=![]() ,
,
∴AK=![]()
∴OK=OA﹣AK=![]() ,
,
∵OG∥CK,
∴△OGM∽△KCM,
∴![]() ,
,
即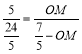 ,
,
∴OM=![]() ,
,
∴AM=5﹣![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
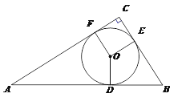
【题目】如图,在Rt△ABC中,∠C=90°,⊙O是Rt△ABC的内切圆,切点为D、E、F.
(1)求证:四边形OECF是正方形;
(2)若AF=10,BE=3,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C(0,﹣3)
(1)求出该抛物线的函数关系式及对称轴
(2)点P是抛物线上的一个动点,设点P的横坐标为t (0<t<3).当△PCB的面积的最大值时,求点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为准矩形.

(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD= ;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是 ;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,身高![]() 都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角 为45,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角 为30.她
都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角 为45,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角 为30.她![]() 们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10 cm,则可计算出塔高约为(结果精确到0.01,参考数据:
们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10 cm,则可计算出塔高约为(结果精确到0.01,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)( ).
≈1.732)( ).
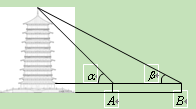
A.36.21米 B.37.71米 C.40.98米 D.42.48米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
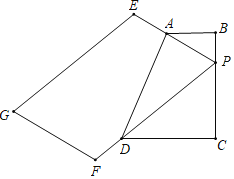
【题目】在四边形ABCD中,AB∥CD,BC⊥CD,AB=2,CD=3,在BC上取点P(P与B、C不重合)连接PA延长至E,使PA=2AE,连接PD并延长至F,使PD=3FD,以PE、PF为边作平行四边形,另一个顶点为G,则PG长度的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
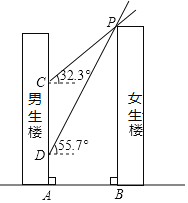
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
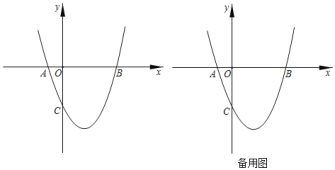
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论:①abc<0;②4a+2b+c>0;③b2-4ac<0;④b>a+c;⑤a+2b+c>0,其中正确的结论有( )
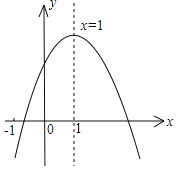
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com