Question

17．古人曾研究过所谓的“多边形数”，即能用点排成多边形（通常排成正多边形）的阵列表示的数，在数学史上曾一度为不少专业和业余的数学家所青睐，人们认为这些奇妙的数一定有它特殊的性质，因为她们的确很具数学美．如图所示是前5个三角形数．第1个三角形数是1，第2个三角形数是3，第3个三角形数是6…，依此规律回答以下三个问题：
（1）第6个三角形数是21；
（2）第n个三角形数是$\frac{n（n+1）}{2}$（用含n的式子表示，其中n表示正整数）；
（3）第2015个三角形数与2013个三角形数的差是4029．

Answer 1

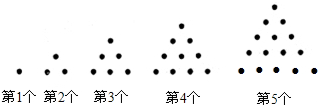
分析 （1）根据“第1个三角形数是1，第2个三角形数是3，第3个三角形数是6…”找到规律，利用规律写出第6个三角形数即可；
（2）根据上题得到的规律用通项公式表示出来即可；
（3）将数据代入求得两个三角形数的差即可

解答 解：（1）第1个三角形数是1，
第2个三角形数是1+2=3，
第3个三角形数是1+2+3=6，
…，
第6个三角形数是1+2+3+4+5+6=21，；

（2）第n个三角形数是1+2+3+…+n=$\frac{n（n+1）}{2}$；

（3）第2013个三角形数与2011个三角形数的差是1+2+3+…+2015-（1+2+3+…+2013）=2015+2014=4029．
故答案为：21，$\frac{n（n+1）}{2}$，4029．

点评 本题考查了图形的变化类问题，解题的关键是仔细观察每个三角形的个数与图形的关系，然后找到通项公式，从而解决问题