
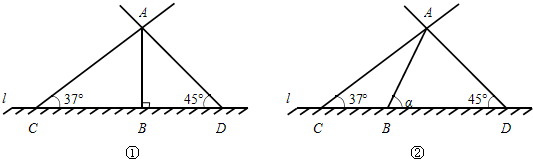
分析 (1)在RT△ABC中,依据正切函数求得BC的长,在△ABD中根据等角对等边求得BD的长,进而就可求得CD的长.
(2)作AE⊥地面于E,在RT△ABE中,依据正弦函数求得AE的长,在RT△AEC中,依据正切函数求得EC的长,在△AED中根据等角对等边求得ED的长,进而就可求得CD的长.
解答 解;(1)在RT△ABC中,∵∠C=37°,
∴BC=$\frac{AB}{tan37°}$=$\frac{6}{0.75}$≈8,
在RT△ABD中,∵∠ADB=45°,
∴∠DAB=∠ADB=45°,
∴BD=AB=6,
∴CD=BC+BD=8+6=14(m);
故答案为14;
(2)作AE⊥地面于E,
在RT△ABE中,∵∠ABE=α,
∴AE=AB•sinα=6•sinα,
在RT△ACE中,∵∠C=37°,
∴CE=$\frac{AE}{tan37°}$=$\frac{6•sinα}{0.75}$≈8•sinα,
在RT△AED中,∵∠ADB=45°,
∴∠DAB=∠ADB=45°,
∴ED=AE=6•sinα,
∴CD=EC+ED=8•sinα+6•sinα=14•sinα(m);
点评 本题考查了学生利用三角函数解决实际问题的能力以及等腰三角形的性质.这就要求学生把实际问题转化为直角三角形的问题,利用三角函数解决问题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
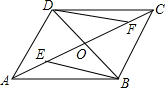 如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.
如图,在平行四边形ABCD中,AC,BD相交于点O,点E,F在AC上,且OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将矩形ABCD(如图)绕点A旋转后,点D落在对角线AC上的点D′,点C落到C′,如果AB=3,BC=4,那么CC′的长为$\sqrt{10}$.
将矩形ABCD(如图)绕点A旋转后,点D落在对角线AC上的点D′,点C落到C′,如果AB=3,BC=4,那么CC′的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com