
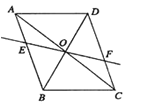
����Ŀ����1����ͼ����ƽ���ı���ABCD�У��Խ���AC,BD���ڵ�O��������O��ֱ�߽�AB��E����CD��F.��֤��OE��OF.
��2����ɳȺ�����ҹ����������������ҹ��Ϻ�����Ҫ����ɳij�����������в�����ҵ�����洬������A��ʱ���õ�λ�����������B����Ϊ�˷�ֹij��Ѳ�����ţ��������ҹ�C������ബǰ��B�����������C��AB�ľ���CDΪ20�����֪Aλ��C������ƫ��60�������ϣ�Bλ��C����ƫ��45���ķ����ϣ� ![]() ��1.7�������ȷ��1�����A��B֮��ľ���.
��1.7�������ȷ��1�����A��B֮��ľ���.
���𰸡���1��֤������������2��A��B��ľ�����(20![]() ��20)����
��20)����
�������������������1������ASA֤����OAE�ա�OCF���Ӷ��õ�OE��OF����2�����ݹ��ɶ������AD��BD�ľ��룬����AB��AD+BD�����AB֮��ľ��룻
���������
(1)֤�������ı���ABCD��ƽ���ı��Σ�
��OA��OC,AB��CD ��
���OAE����OCF
�ߡ�AOE����COF ��
���OAE�ա�OCF
��OE��OF
��2���⣺��CD��AB����ACD��600 ��
���A��300
��CD��20��
��AD��20![]()
��CD��AB, ��BCD��450��
���B��450 ��
��CD��BD��20
��AB�� AD�� BD��20![]() ��20(����)
��20(����)


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�Dz����������Σ����߶�AD�ѡ�ABC��Ϊ�����ȵ������֣����߶�ADӦ���ǣ� ��
A.�����εĽ�ƽ����
B.���������
C.�����εĸ�
D.���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������̣��������ڵĺ�������ջ������������ݣ�
��ͼ����֪��AB��EF��EP��EQ����EQC+��APE=90�㣬��֤��AB��CD
֤������AB��EF
���APE=����
��EP��EQ
���PEQ=����
����QEF+��PEF=90��
���APE+��QEF=90��
�ߡ�EQC+��APE=90��
���EQC=
��EF������
��AB��CD����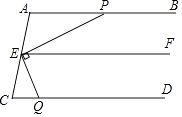
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB=4cm��BC=3cm��CD=12cm��DA=13cm���ҡ�ABC=90�㣬���ı���ABCD�����Ϊ�� �� 
A.6cm2
B.30cm2
C.24cm2
D.36cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCD�У��Խ���AC��BD���ڵ�O����BAD=120�㣬AC=4��������ε�����ǣ� ��
A.16 ![]()
B.16
C.8 ![]()
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��ΪDF�ϵĵ㣬BΪAC�ϵĵ㣬��1=��2����C=��D����˵����AC��DF��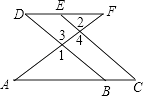
�⣺�ߡ�1=��2����֪����
��1=��3������
���2=��3��������������
������ͬλ����ȣ���ֱ��ƽ�У���
���C=��ABD ������
�֡ߡ�C=��D����֪����
���D=��ABD��������������
��AC��DF������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У���E��F�ڶԽ���BD�ϣ���BE=DF����֤�� 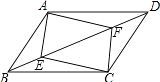
��1��AE=CF��
��2���ı���AECF��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
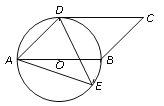
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ���ABΪֱ���ġ�O������D��E�ǡ�O��һ�㣬�ҡ�AED=45��
(1)���ж�CD���O��λ�ù�ϵ����֤����Ľ��ۣ�
(2)����O�İ뾶Ϊ3��sin��ADE=![]() ����AE��ֵ��
����AE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��cΪ��ABC�����ߣ���a2c2��b2c2=a4��b4����������ε���״Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com