
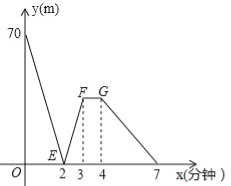
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.
【答案】(1)70米,95米/分;(2)y=35x﹣70;(3)490米;(4):两机器人出发1.2s或2.8s或4.8s相距28米.
【解析】
试题分析:(1)结合图象得到A、B两点之间的距离,甲机器人前2分钟的速度;(2)根据题意求出点F的坐标,利用待定系数法求出EF所在直线的函数解析式;(3)根据一次函数的图象和性质解答;(4)根据速度和时间的关系计算即可;(5)分前2分钟、2分钟﹣3分钟、4分钟﹣7分钟三个时间段解答.
试题解析:(1)由图象可知,A、B两点之间的距离是70米,
甲机器人前2分钟的速度为:(70+60×2)÷2=95米/分;
(2)设线段EF所在直线的函数解析式为:y=kx+b,
∵1×(95﹣60)=35,
∴点F的坐标为(3,35),
则![]() ,
,
解得,![]() ,
,
∴线段EF所在直线的函数解析式为y=35x﹣70;
(3)∵线段FG∥x轴,
∴甲、乙两机器人的速度都是60米/分;
(4)A、C两点之间的距离为70+60×7=490米;
(5)设前2分钟,两机器人出发xs相距28米,
由题意得,60x+70﹣95x=28,
解得,x=1.2,
前2分钟﹣3分钟,两机器人相距28米时,
35x﹣70=28,
解得,x=2.8,
4分钟﹣7分钟,两机器人相距28米时,
(95﹣60)x=28,
解得,x=0.8,
0.8+4=4.8,
答:两机器人出发1.2s或2.8s或4.8s相距28米.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。

(1)求证:四边形CMAN是平行四边形。
(2)已知DE=4,FN=3,求BN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角形的两条直角边分别为12cm和16cm,则这个直角三角形内切圆的半径是( )
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面证明:

(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b.
证明:∵a⊥c (已知)
∴∠1= (垂直定义)
∵b∥c (已知)
∴∠1=∠2 ( )
∴∠2=∠1=90° ( )
∴a⊥b ( )
(2)如图2:AB∥CD,∠B+∠D=180°,求证:CB∥DE.
证明:∵AB∥CD (已知)
∴∠B= ( )
∵∠B+∠D=180° (已知)
∴∠C+∠D=180° ( )
∴CB∥DE ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com