
 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为y.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为y.分析 (1)由矩形的性质及平移的性质易得∠A1=∠DAC,A1D1=AD,AA1=CC1,结论显然;
(2)由所给条件可证明△AC1B是等边三角形,ABC1D1自然是菱形;
(3)由△AC1F∽△ACD可得面积之比等于相似比的平方,利用这一等量关系列出等式,变形即得所求关系式.
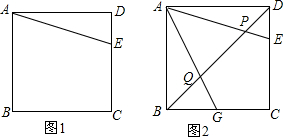
解答 解:(1)如图1,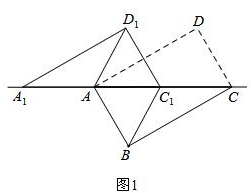
∵四边形ABCD为矩形,
∴BC=AD,BC∥AD,
∴∠DAC=∠ACB,
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,$\left\{\begin{array}{l}{A{A}_{1}=C{C}_{1}}\\{∠{A}_{1}=∠ACB}\\{{A}_{1}{D}_{1}=CB}\end{array}\right.$,
∴△A1AD≌△CC1B;
(2)如图2,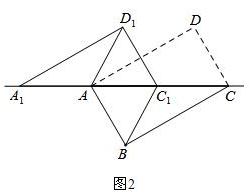
∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,
∴△AC1B是等边三角形,
∴AB=D1C1,
又AB∥BC1,
∴四边形ABC1D1是菱形;
(3)如图3,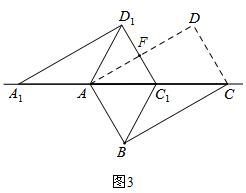
∵C1D1∥CD,
∴△AC1F∽△ACD,
∴$\frac{{S}_{△A{C}_{1}F}}{{S}_{△ACD}}=(\frac{2-x}{2})^{2}$,
解得:$y=\frac{\sqrt{3}}{8}(2-x)^{2}$.
点评 本题考查了矩形的性质、平移变换、全等三角形的判定与性质、等边三角形的判定与性质、菱形的判定、相似三角形的判定与性质等知识点,综合性较强,难度中等.清楚矩形、菱形等基本几何图形的性质以及平移变换的特征是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
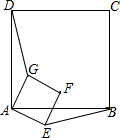 如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.
如图,正方形ABCD与正方形AEFG有公共顶点A,当正方形AEFG绕着点A顺时针旋转时,在图中你能否找到一条线段与线段DG相等,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-5,b=-3 | B. | a=3,b=3 | C. | a=-3,b=-3 | D. | a=-3,b=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com