练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．若关于x的分是方程$\frac{2}{x-3}+\frac{mx}{3-x}$=2有增根，则m的值是$\frac{2}{3}$．

    分析 分式方程去分母转化为整式方程，由分式方程有增根，得到x-3=0，求出x的值，代入整式方程即可求出m的值．

    解答 解：去分母得：2-mx=2x-6，
    由分式方程有增根，得到x-3=0，即x=3，
    把x=3代入整式方程得：2-3m=0，
    解得：m=$\frac{2}{3}$，
    故答案为：$\frac{2}{3}$

    点评 此题考查了分式方程的增根，增根问题可按如下步骤进行：①让最简公分母为0确定增根；②化分式方程为整式方程；③把增根代入整式方程即可求得相关字母的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

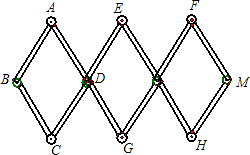    1．如图，用3个全等的菱形构成活动衣帽架，顶点A、E、F、C、G、H是上、下两排挂钩，根据需要可以改变挂钩之间的距离（比如AC两点可以自由上下活动），若菱形的边长为13厘米，要使两排挂钩之间的距离为24厘米，并在点B、M处固定，则B、M之间的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

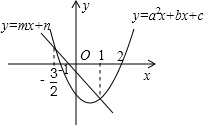    2．已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示，且抛物线与x轴交于点（-1，0）、（2，0），抛物线与直线交点的横坐标为1和-$\frac{3}{2}$，那么不等式mx+n＜ax2+bx+c＜0的解集是（　　）
    A．1＜x＜2B．x＜-$\frac{3}{2}$或x＞1C．-$\frac{3}{2}$＜x＜2D．-1＜x＜2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．已知直线y=k（x-3）经过点（4，1），那么k=1；若另一直线l与直线y=k（x-3）平行，且它们之间的距离为1，则直线l的解析式为y=x-3-$\sqrt{2}$或y=x-3+$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（-$\frac{2}{9}$）×（-18）+（-$\frac{5}{11}$）×（-3）×2$\frac{1}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．若a=-2×53，b=（-2×5）3，c=-23×（-5）3，则下列大小关系中正确的是（　　）
    A．c＞a＞bB．a＞c＞bC．b＞c＞aD．a＞b＞c

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

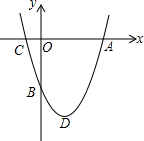    3．如图，抛物线y=x2+bx-c和x轴交于A，C两点，和y轴交于B点，抛物线的顶点为D，OA=OB=3．
    （1）求此抛物线的解析式、顶点D的坐标和对称轴；
    （2）点P为x轴下方抛物线上的一个点，求使S△ACP=S△AOD的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，菱形ABCD的边长为2，∠ABC=45°，则点A的坐标为（$\sqrt{2}$，$\sqrt{2}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连结AD1、BC1．已知∠ACB=30°，AB=1，CC1=x，△ACD与△A1C1D1重叠部分的面积为y．
    （1）求证：△A1AD1≌△CC1B；
    （2）当x=1时，求证：四边形ABC1D1是菱形；
    （3）求y关于x的函数关系式．

    查看答案和解析>>

    同步练习册答案