
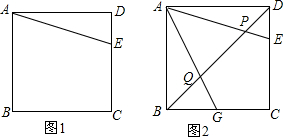
分析 (1)过点A作AE'⊥AE交CB的延长线于点E',则△ABE'就是旋转后的图形,直接作图即可;
(2)作∠EAE′的平分线交BC于点F,可证EF=BF+DE,则△CFE的周长等于正方形ABCD的周长的一半;
(3)作BM⊥BD,BM=PD,连AM,依次证明△ADP≌△ABM,△MAQ≌△PAQ,得出△MBQ是直角三角形,结论显然.
解答 解:(1)如图1所示:△ABE′即为所求;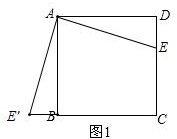
(2)作∠EAE′的平分线交BC于点F,则△CFE的周长等于正方形ABCD的周长的一半,如图2,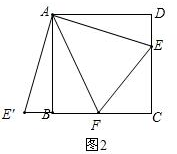
在△AEF和△AE′F中:
∵AE=AE′,
∠EAF=∠E′AF,
AF=AF,
∴△AEF≌△AE′F(SAS),
∴EF=E′F=BF+DE,
∴EF+EC+FC=BC+CD.
(3)作BM⊥BD,BM=PD,连AM,如图3,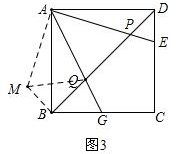
易证△ADP≌△ABM(SAS),
∴AM=AP,∠BAM=∠DAP,∠MBA=∠PDA=45°,
∵∠PAQ=45°,
∴∠DAP+∠BAQ=∠BAM+∠BAQ=45°,
即∠MAQ=45°,
易证△MAQ≌△PAQ(SAS),
∴MQ=PQ,
∵∠MBQ=∠MBA+∠ABD=90°,
∴MQ2=BM2+BQ2,
∴PQ2=PD2+BQ2.
点评 本题考查了旋转变换、正方形的性质、全等三角形的判定与性质、勾股定理等知识点,难度中等.本题是经典“大角夹半角”模型,高频考点,务必掌握.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
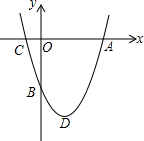 如图,抛物线y=x2+bx-c和x轴交于A,C两点,和y轴交于B点,抛物线的顶点为D,OA=OB=3.
如图,抛物线y=x2+bx-c和x轴交于A,C两点,和y轴交于B点,抛物线的顶点为D,OA=OB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为y.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
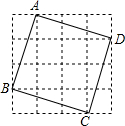 如图,由16个边长为1的小正方形构成的网格图中,有一个正方形(图中实线表示)
如图,由16个边长为1的小正方形构成的网格图中,有一个正方形(图中实线表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com