练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

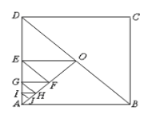
    【题目】如图，在边长为1的正方形中，当第1次作，第2次作；第3次作，……依次方法继续作垂直线段，当作到第10次时，所得的最小的三角形的面积是（ ）

    A.B.C.D.

    【答案】B

    【解析】

    根据正方形的性质可得AB=AD，然后根据等腰直角三角形的性质求出△AOD的面积，再求出△AOE的面积，△AEF的面积，根据计算结果可得下一次得到最小的三角形的面积是上一次三角形的，然后写出第10次时所得的最小的三角形的面积即可．

    ∵四边形ABCD是正方形，边长为1，

    ∴AB=AD，正方形的面积为1，

    第1次作AO⊥BD,则最小△AOD的面积=××1==，

    第2次作EO⊥AD,最小△AOE的面积=×==；

    第3次作EF⊥AO,最小△AEF的面积=×=，

    …，

    依此类推,作到第10次时,最小三角形的面积=.

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某科研小组计划对某一品种的西瓜用两种种植技术种植．在选择种植技术时，该科研小组主要关心的问题是：西瓜的产量和产量的稳定性，以及西瓜的优等品率．为了解这两种种植技术种出的西瓜的质量情况，科研小组各对两块自然条件相同的试验田进行对比试验，并从这两块实验田中随机抽取20个西瓜，分别称重后，将称重的结果记录如下：

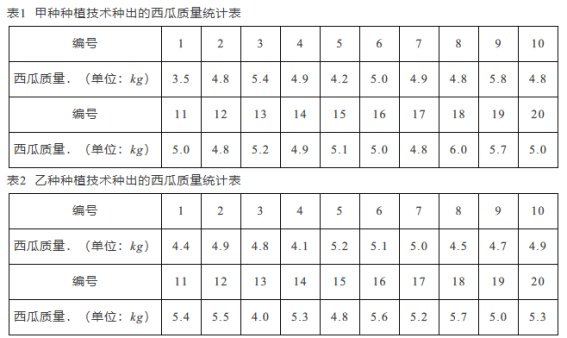
    回答下列问题：

    （1）若将质量为4．5～5．5（单位：kg）的西瓜记为优等品，完成下表：

    优等品西瓜个数

    平均数

    方差

    甲种种植技术种出的西瓜质量

    4．98

    0．27

    乙种种植技术种出的西瓜质量

    15

    4．97

    0．21

    （2）根据以上数据，你认为该科研小组应选择哪种种植技术?并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】温州某企业安排名工人生产甲、乙两种产品，每人每天生产件甲或件乙，甲产品每件可获利元.根据市场需求和生产经验，乙产品每天产量不少于件，当每天生产件时，每件可获利元， 每增加件，当天平均每件利润减少元.设每天安排人生产乙产品.

    根据信息填表：

    产品种类

    每天工人数(人)

    每天产量(件)

    每件产品可获利润(元)

    甲

    __________

    _____________

    乙

    _____________

    若每天生产甲产品可获得的利润比生产乙产品可获得的利润多元，求每件乙产品可获得的利润.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

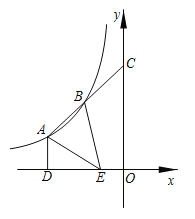
    【题目】如图，A，B是反比例函数(k≠0)图象上的两点，延长线段AB交y轴于点C，且B为线段AC的中点，过点A作AD⊥x轴于点D，E为线段OD的三等分点，且OE＜DE．连接AE，BE．若S△ABE＝7，则k的值为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

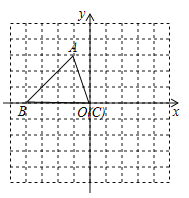
    【题目】（2016黑龙江省齐齐哈尔市）如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣1，3），B（﹣4，0），C（0，0）

    （1）画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A1B1C1；

    （2）画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O；

    （3）在x轴上存在一点P，满足点P到A1与点A2距离之和最小，请直接写出P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴、轴分别相交于、两点；分别过、两点作轴、轴的垂线相交于点.为边上一动点．

    　　

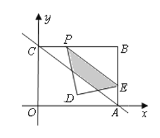
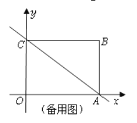
    （1）求三角形的面积；

    （2）点从点出发沿着以每秒1个单位长度的速度向点匀速运动，过点作交于，设运动时间为秒.用含的代数式表示的面积；

    （3）在（2）的条件下点的运动过程中，将沿着折叠（如图所示），点在平面内的落点为点．当与重叠部分的面积等于时，试求出点的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，钝角△ABC中，AB=AC，BC=2，O是边AB上一点，以O为圆心，OB为半径作⊙O，交边AB于点D，交边BC于点E，过E作⊙O的切线交边AC于点F．

    （1）求证：EF⊥AC．

    （2）连结DF，若∠ABC=30°，且DF∥BC，求⊙O的半径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某宾馆有客房间供游客居住，当每间客房的定价为每天元时，客房恰好全部住满；如果每间客房每天的定价每增加元，就会减少间客房出租．设每间客房每天的定价增加元，宾馆出租的客房为间．求：

    关于的函数关系式；

    如果某天宾馆客房收入元，那么这天每间客房的价格是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＝4，BC＝8，把△ABC沿着AC向上翻折得到△AEC，EC交AD边于点F，则点F到AC的距离是_____．

    查看答案和解析>>

    同步练习册答案