
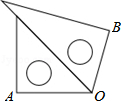
 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )| A. | 60° | B. | 75° | C. | 105° | D. | 180° |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 轮船在点O测得岛A在北偏东60°,距离为4千米,又测得测得岛B在点O北偏西30°,距离为3千米.①用1厘米代表1千米,画出A、B的位置.②量出图上线段AB的长度.
轮船在点O测得岛A在北偏东60°,距离为4千米,又测得测得岛B在点O北偏西30°,距离为3千米.①用1厘米代表1千米,画出A、B的位置.②量出图上线段AB的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)【阅读理解】
(1)【阅读理解】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com