
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边中点,过D点作DE⊥DF,分别交边AB、BC于点E、F,连接BD.

(1)求证:△BDE≌△CDF.
(2)若AE=4,FC=3,求EF长.
【答案】(1)见解析;(2)EF=5.
【解析】
(1)由等腰直角三角形ABC中,D为AC边上中点,知BD⊥AC,BD=CD=AD,∠ABD=45°,然后通过角度转换得到∠FDC=∠EDB,即可证明全等;
(2)由△BED≌△CFD就可以得出AE=BF,BE=CF,即可求得EF的长.
(1)∵等腰直角三角形ABC中,D为AC边上中点,
∴BD⊥AC(三线合一),BD=CD=AD,∠ABD=45°,
∴∠C=45°,
∴∠ABD=∠C,
又∵DE丄DF,
∴∠FDC+∠BDF=∠EDB+∠BDF,
∴∠FDC=∠EDB,
在△EDB与△FDC中,
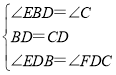
∴△EDB≌△FDC(ASA);
(2)∵△EDB≌△FDC,
∴BE=FC=3,
∴AB=AE+BE=4+3=7,则BC=7,
∴BF=4,
在Rt△EBF中,![]() .
.


科目:初中数学 来源: 题型:
【题目】某校举办“打造平安校园”活动,随机抽取了部分学生进行校园安全知识测试![]() 将这些学生的测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘制成如下统计图
将这些学生的测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘制成如下统计图![]() 请你根据图中信息,解答下列问题:
请你根据图中信息,解答下列问题:

![]() 本次参加校园安全知识测试的学生有多少人?
本次参加校园安全知识测试的学生有多少人?
![]() 计算B级所在扇形圆心角的度数,并补全折线统计图;
计算B级所在扇形圆心角的度数,并补全折线统计图;
![]() 若该校有学生1000名,请根据测试结果,估计该校达到及格和及格以上的学生共有多少人?
若该校有学生1000名,请根据测试结果,估计该校达到及格和及格以上的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如图,在△ABC中,∠C=90,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.

(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学进行登山比赛,甲同学和乙同学沿相同的路线同时在早8:00从山脚出发前往山顶,甲同学到达山顶后休息1小时,沿原路以每小时6千米的速度下山,在这一过程中,各自行进的路程随所用时间变化的图象如图所示,根据提供信息得出以下四个结论:
![]() 甲同学从山脚到达山顶的路程为12千米;
甲同学从山脚到达山顶的路程为12千米;
![]() 乙同学登山共用4小时;
乙同学登山共用4小时;
![]() 甲同学在14:00返回山脚;
甲同学在14:00返回山脚;
![]() 甲同学返回与乙同学相遇时,乙同学距登到山顶还有
甲同学返回与乙同学相遇时,乙同学距登到山顶还有![]() 千米的路程.
千米的路程.
以上四个结论正确的有![]()
![]() 个
个
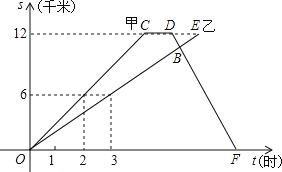
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.

(1)请画出此时小丽在阳光下的影子;
(2)若已知小明的身高为1.60 m,小明和小丽之间的距离为2 m,而小丽的影子长为1.75 m,求小丽的身高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值
(1)(2x+1)2﹣4(x﹣1)(x+1),其中x=![]() ;
;
(2)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷(2x),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,给出如下定义:记点P到x轴的距离为![]() ,到y轴的距离为
,到y轴的距离为![]() ,若
,若![]() ,则称
,则称![]() 为点P的最大距离;若
为点P的最大距离;若![]() ,则称
,则称![]() 为点P的最大距离.
为点P的最大距离.
例如:点P(![]() ,
,![]() )到到x轴的距离为4,到y轴的距离为3,因为3 < 4,所以点P的最大距离为
)到到x轴的距离为4,到y轴的距离为3,因为3 < 4,所以点P的最大距离为![]() .
.
(1)①点A(2,![]() )的最大距离为 ;
)的最大距离为 ;
②若点B(![]() ,
,![]() )的最大距离为
)的最大距离为![]() ,则
,则![]() 的值为 ;
的值为 ;
(2)若点C在直线![]() 上,且点C的最大距离为
上,且点C的最大距离为![]() ,求点C的坐标;
,求点C的坐标;

(3)若⊙O上存在点M,使点M的最大距离为![]() ,直接写出⊙O的半径r的取值范围.
,直接写出⊙O的半径r的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com