
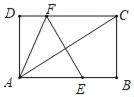
【题目】如图,EF垂直平分矩形ABCD的对角线AC,与AB、CD分别交于点E、F,连接AF.已知AC=4,设AB=x,AF=y,则y关于x的函数关系用图象大致可以表示为( )
A.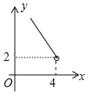 B.
B.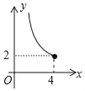 C.
C.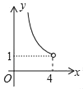 D.
D.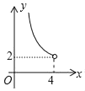
【答案】D
【解析】
先由自变量x的取值,函数y的最小值,排除掉选项B和C,再得出y为关于x的反比例函数,排除A,从而得正确答案.
解:由AB<AC=4可知,B错误;
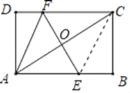
由EF垂直平分矩形ABCD的对角线AC,得FA=FC,连接EC,则EC=EA,
易证△CFO≌△AEO(ASA)
∴AE=CF=AF=CE=y,BE=AB﹣AE=x﹣y,
∵在直角三角形AEO中,AE>AO=![]() ,
,
∴y>2,排除C;
在直角三角形ABC和直角三角形ECB中,
由勾股定理可得:AC2﹣AB2=EC2﹣BE2,
16﹣x2=y2﹣(x﹣y)2,
化简得:xy=8,
∴![]() ,故y为关于x的反比例函数,排除A;
,故y为关于x的反比例函数,排除A;
综上,D正确.
故选:D.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角![]() 为
为![]() ,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角
,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角![]() 为
为![]() ,点A、B、C三点在同一水平线上.
,点A、B、C三点在同一水平线上.
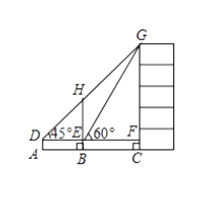
(1)求古树BH的高;
(2)求教学楼CG的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
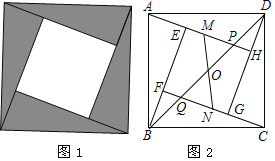
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 在射线
在射线![]() 上,把线段
上,把线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .请根据题意画出图形并完成下列问题:
.请根据题意画出图形并完成下列问题:
(1)求![]() 的长;
的长;
(2)设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的横坐标
的横坐标![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在毕业晚会上,同学们表演哪一类型的节目由自己摸球来决定.在一个不透明的口袋中,装有除标号外其它完全相同的A、B、C三个小球,表演节目前,先从袋中摸球一次(摸球后又放回袋中),如果摸到的是A球,则表演唱歌;如果摸到的是B球,则表演跳舞;如果摸到的是C球,则表演朗诵.若小明要表演两个节目,则他表演的节目不是同一类型的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y=![]() 的图象交于点C(﹣1,m).
的图象交于点C(﹣1,m).
(1)求一次函数和反比例函数的表达式;
(2)直接写出关于x的不等式2x+b>![]() 的解集;
的解集;
(3)点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”活动.经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,最终没有学生得分低于25分,也没有学生得满分.根据测试成绩绘制出频数分布表和频数分布直方图(如图).
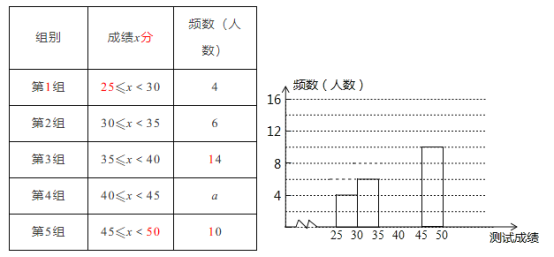
请结合图标完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若本次决赛的前5名是3名女生A、B、C和2名男生M、N,若从3名女生和2名男生中分别抽取1人参加市里的比赛,试用列表法或画树状图的方法求出恰好抽到女生A和男生M的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).
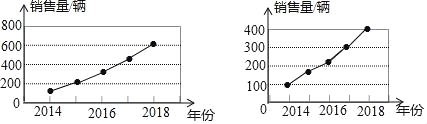
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y=![]() 的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com