
【题目】在平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 在射线
在射线![]() 上,把线段
上,把线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .请根据题意画出图形并完成下列问题:
.请根据题意画出图形并完成下列问题:
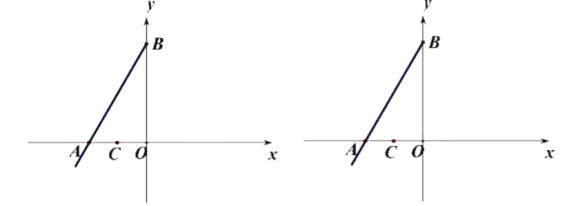
(1)求![]() 的长;
的长;
(2)设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的关系式;
的关系式;
(3)在(2)的条件下,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,当
,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的横坐标
的横坐标![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)﹣5或-1或3.
;(3)﹣5或-1或3.
【解析】
(1)在Rt△ABO中,根据OA=4,∠BAO=60°解直角三角形即可得到AB的长.作图分两种情况:①点D在A的下方,②点D在线段AB上;
(2)分三种情况讨论:①当D在A的下方时,作CM⊥AB于M,EN⊥OA于N.
由点D的横坐标为t,A的横坐标为-4,得出t<-4.用待定系数法求出直线AB的解析式为y![]() x+4
x+4![]() .设D(t,
.设D(t,![]() t+4
t+4![]() ).通过证明△CDM≌△ECN,得到EN=CM,CN=DM.解直角三角形CAM得到AM,CM的长.利用两点间距离公式得到AD
).通过证明△CDM≌△ECN,得到EN=CM,CN=DM.解直角三角形CAM得到AM,CM的长.利用两点间距离公式得到AD![]() .由t<-4,得到AD=﹣8﹣2t,DM=﹣7﹣2t,CN=DM=﹣7﹣2t,ON=﹣5﹣2t,即可得到结论;
.由t<-4,得到AD=﹣8﹣2t,DM=﹣7﹣2t,CN=DM=﹣7﹣2t,ON=﹣5﹣2t,即可得到结论;
②当D在A的上方线段AB上,E在第二象限时,作CM⊥AB于M,EN⊥OA于N.由点D的横坐标为t,A的横坐标为-4,得到t>-4.同①可得:AM=1,CM=![]() ,AD=
,AD=![]() =8+2t,DM=7+2t,CN=DM=7+2t,ON=﹣5﹣2t,即可得到结论;
=8+2t,DM=7+2t,CN=DM=7+2t,ON=﹣5﹣2t,即可得到结论;
③当D在A的上方线段AB上,E在第一象限时,同②可得结论;
(3)连接EF、FC、DF.设EC和DF相交于点H.证明四边形DCFE是菱形,得到H平分DF和EC.设F(x,y).由中点坐标公式可得x,y的值,从而得到F的坐标,表示出![]() ,
,![]() ,
,![]() ,然后分三种情况讨论,解方程即可.
,然后分三种情况讨论,解方程即可.
(1)∵C(﹣2,0),
∴OC=2.
∵C为OA的中点,
∴OA=2OC=4.
∵∠BAO=60°,
∴∠ABO=30°,
∴OB=![]() AC=
AC=![]() ,AB=2AO=8;
,AB=2AO=8;
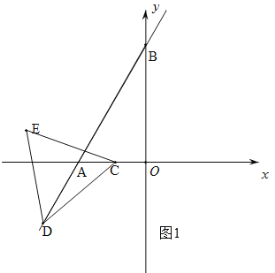
作图分两种情况:①点D在A的下方,如图1;②点D在线段AB上,如图2.
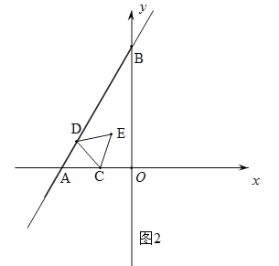
(2)分三种情况讨论:①当D在A的下方时,如图3.
作CM⊥AB于M,EN⊥OA于N.
∵点D的横坐标为t,A的横坐标为-4,
∴t<-4.
∵B(0,4![]() ),A(﹣4,0),
),A(﹣4,0),
∴设直线AB的解析式为![]() ,把A(﹣4,0)代入得:
,把A(﹣4,0)代入得:![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y![]() x+4
x+4![]() .
.
设D(t,![]() t+4
t+4![]() ).
).
∵∠DCE=∠BAC=60°,
∴∠ECN+∠ACD=∠ACD+∠CDM,
∴∠CDM=∠ECN,
在△CDM和△ECN中,
 ,
,
∴△CDM≌△ECN,
∴EN=CM,CN=DM.
∵AC=2,∠CAM=60°,
∴AM=1,CM=![]() .
.
∵D(t,![]() t+4
t+4![]() ),A(-4,0),
),A(-4,0),
∴AD=![]() .
.
∵t<-4,
∴AD=﹣8﹣2t,
∴DM=﹣7﹣2t,
∴CN=DM=﹣7﹣2t,
∴ON=﹣5﹣2t,
∴点E坐标(2t+5,![]() ),
),
∴E点横坐标d=2t+5,
②当D在A的上方线段AB上,E在第二象限时,如图4,作CM⊥AB于M,EN⊥OA于N.
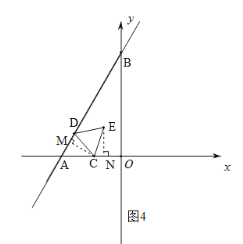
∵点D的横坐标为t,A的横坐标为-4,
∴t>-4.
同①可得:直线AB的解析式为y![]() x+4
x+4![]() ,AM=1,CM=
,AM=1,CM=![]() ,AD=
,AD=![]() .
.
∵t>-4
∴AD=8+2t,DM=7+2t,
∴CN=DM=7+2t,
∴ON=OC-CN=2-(7+2t)=﹣5﹣2t,
∴点E坐标(2t+5,![]() ),
),
∴E点横坐标d=2t+5.
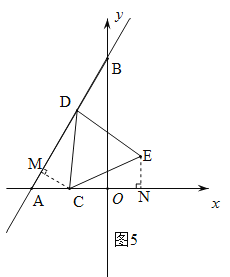
③当D在A的上方线段AB上,E在第一象限时,如图5,作CM⊥AB于M,EN⊥OA于N.
∵点D的横坐标为t,A的横坐标为-4,
∴t>-4.
同②可得:直线AB的解析式为y![]() x+4
x+4![]() ,AM=1,CM=
,AM=1,CM=![]() ,AD=
,AD=![]() .
.
∵t>-4,
∴AD=8+2t,DM=7+2t,
∴CN=DM=7+2t,
∴ON=CN-OC=(7+2t)-2=2t+5,
∴点E坐标(2t+5,![]() ),
),
∴E点横坐标d=2t+5.
综上所述:E点横坐标d=2t+5.
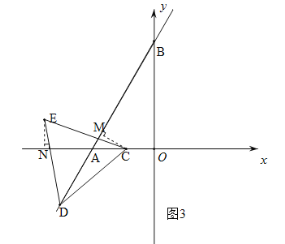
(3)如图6,连接EF、FC、DF.设EC和DF相交于点H.
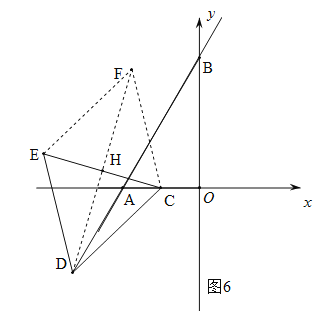
∵D、F关于直线EC对称,
∴DE=EF,DC=CF.
∵△DCE是等边三角形,
∴DE=DC,
∴DE=DC=FC=EF=EC,
∴四边形DCFE是菱形,
∴H平分DF和EC.
设F(x,y).
∵C(﹣2,0),E(2t+5,![]() ),D(t,
),D(t,![]() t+4
t+4![]() ),
),
∴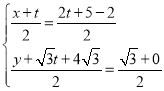 ,
,
解得: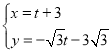 ,
,
∴D关于CE的对称点F点的坐标为(t+3,![]() ).
).
∵A(-4,0),F(t+3,![]() )
)
∴![]() =16,
=16,![]() =
=![]() ,
,
![]() =
=![]() =
=![]() .
.
∵△OAF是等腰三角形,
∴分三种情况讨论:
①当OA=OF时,![]() =
=![]() ,
,
∴![]() ,
,
解得:t=-5或t=-1,
∴d=2t+5=-5或3;
②当OF=AF时,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:t=-5,
∴d=2t+5=-5;
③当AF=OA时,![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:t=-3或t=-5,
∴d=2t+5=-1或-5.
综上所述:d的值为-5或-1或3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
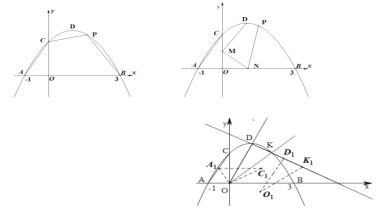
【题目】如图,抛物线![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 点的右侧),与
点的右侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线的顶点,且
为抛物线的顶点,且![]() .
.
(1)点![]() 为直线
为直线![]() 上方抛物线上一点,求四边形
上方抛物线上一点,求四边形![]() 的面积的最大值;点
的面积的最大值;点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 上的动点,当四边形
上的动点,当四边形![]() 面积取得最大值时,求当线段
面积取得最大值时,求当线段![]() 的值为最小值时点
的值为最小值时点![]() 的坐标.
的坐标.
(2)把![]() 绕点
绕点![]() 旋转一定角度后得到
旋转一定角度后得到![]() ,且点
,且点![]() 恰好在线段
恰好在线段![]() 上,抛物线上的点
上,抛物线上的点![]() 与点
与点![]() 关于抛物线对称轴对称,作
关于抛物线对称轴对称,作![]() ,把
,把![]() 沿直线
沿直线![]() 平移后得到
平移后得到![]() ,在变换过程中是否存在
,在变换过程中是否存在![]() 为等腰三角形,若存在,直接写出此时
为等腰三角形,若存在,直接写出此时![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
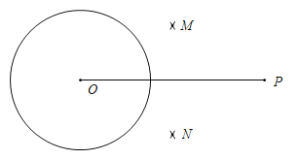
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅(购买的数量不超过8吨),包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(单位:吨)之间的函数关系如图所示.
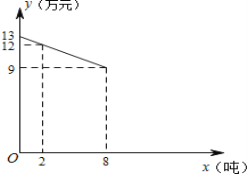
(1)求y与x的函数表达式?
(2)当销售数量为多少时,该公司经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)
(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是![]()
①当该公司销售杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?
②该公司销售杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
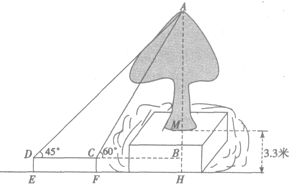
【题目】西安市某中学数学兴趣小组在开展“保护环境,爱护树木”的活动中,利用课外时间测量一棵古树的高,由于树的周围有水池,同学们在低于树基3.3米的一平坝内(如图).测得树顶A的仰角∠ACB=60°,沿直线BC后退6米到点D,又测得树顶A的仰角∠ADB=45°.若测角仪DE高1.3米,求这棵树的高AM.(结果保留两位小数,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
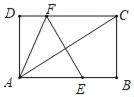
【题目】如图,EF垂直平分矩形ABCD的对角线AC,与AB、CD分别交于点E、F,连接AF.已知AC=4,设AB=x,AF=y,则y关于x的函数关系用图象大致可以表示为( )
A.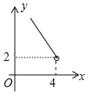 B.
B.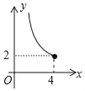 C.
C.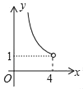 D.
D.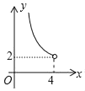
查看答案和解析>>
科目:初中数学 来源: 题型:
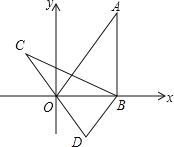
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为( )
A.(﹣2,2![]() )B.(﹣4,2
)B.(﹣4,2![]() )C.(﹣2
)C.(﹣2![]() ,2)D.(﹣2
,2)D.(﹣2![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com