
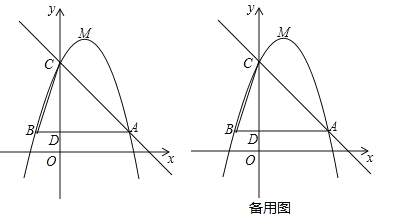
����Ŀ����ͼ����֪���κ���![]() ��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ������ڡ�ABC���ڲ�����������ABC�ı߽磩����m��ȡֵ��Χ��
��3����P��ֱ��AC�ϵĶ��㣬����P����C����M�����ɵ����������BCD���ƣ���ֱ��д�����е�P�����ֱ꣨��д�����������д�����̣���
���𰸡���1��![]() ��M��1��5������2��2��m��4����3��P1��
��M��1��5������2��2��m��4����3��P1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����
��������
�����������1������A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ
��2����M�����ŶԳ���ֱ��x=1����ƽ�Ƶģ��������ֱ��AC�Ľ���ʽ����x=1���������M������ƽ��ʱ��AC��AB�ཻʱy��ֵ�����ɵõ�m��ȡֵ��Χ��
��3������������ɵá�MCP=90�㣬������PCM���BCD���ƣ���Ҫ���з������ۣ��ֳɡ�PCM�ס�BDC���PCM�ס�CDB���֣�Ȼ�����ñߵĶ�Ӧ��ֵ��������꣮
�����������1���ѵ�A��3��1������C��0��4��������κ���![]() ������
������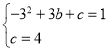 �����
�����![]() �������κ�������ʽΪ
�������κ�������ʽΪ![]() ���䷽��
���䷽��![]() ������M������Ϊ��1��5����
������M��������1��5����
��2����ֱ��AC����ʽΪy=kx+b���ѵ�A��3��1����C��0��4���������![]() �����
�����![]() ����ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F��
����ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F��
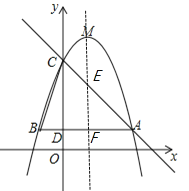
��x=1����ֱ��AC����ʽy=��x+4���y=3�����E����Ϊ��1��3������F����Ϊ��1��1������1��5��m��3�����2��m��4��
��3������MC����MG��y�Ტ�ӳ���AC�ڵ�N�����G����Ϊ��0��5����
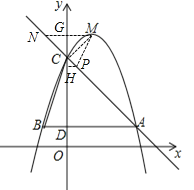
��MG=1��GC=5��4=1����MC=![]() =
=![]() =
=![]() ����y=5����y=��x+4���x=��1�����N����Ϊ����1��5������NG=GC��GM=GC������NCG=��GCM=45�㣬����NCM=90�㣬�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ����
����y=5����y=��x+4���x=��1�����N����Ϊ����1��5������NG=GC��GM=GC������NCG=��GCM=45�㣬����NCM=90�㣬�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ����
�����С�PCM�ס�BDC������![]() ����BD=1��CD=3����CP=
����BD=1��CD=3����CP=![]() =
=![]() =
=![]() ����CD=DA=3������DCA=45�㣬����P��y���Ҳ࣬��PH��y�ᣬ����PCH=45�㣬CP=
����CD=DA=3������DCA=45�㣬����P��y���Ҳ࣬��PH��y�ᣬ����PCH=45�㣬CP=![]() ��span>��PH=
��span>��PH=![]() =
=![]() ����x=
����x=![]() ����y=��x+4�����y=
����y=��x+4�����y=![]() ����P1��
����P1��![]() ��
��![]() ����
����
ͬ���ɵã�����P��y����࣬���x=![]() ����y=��x+4�����y=
����y=��x+4�����y=![]() ����P2��
����P2��![]() ��
��![]() ����
����
�����С�PCM�ס�CDB������![]() ����CP=
����CP=![]() =
=![]() ����PH=
����PH=![]() =3��
=3��
����P��y���Ҳ࣬��x=3����y=��x+4�����y=1��
����P��y����࣬��x=��3����y=��x+4�����y=7
��P3��3��1����P4����3��7���������з�������õ�P������4�����ֱ�ΪP1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧС���ͬѧΪ�˽⡰�Ķ����䡱��Ŀ�չ��������������50��ͬѧ��������һ�ܵ��Ķ�ʱ�������ͳ�ƣ������Ƴ���ͼ��ʾ������ͳ��ͼ���������ݵ���λ���������ֱ��ǣ� ��
A.��λ������������8Сʱ
B.��λ����25�ˣ�������20��
C.��λ����13�ˣ�������20��
D.��λ����6Сʱ��������8Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
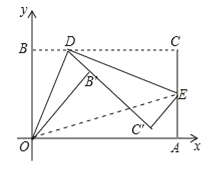
����Ŀ����ͼ��������ֽƬABCD����ֱ������ϵ�У���A��4��0������B��0��3������D�����ڵ�B��C��Ϊ��BC�϶��㣬����O��D�۵�ֽƬ���õ�B����ۺ�OD������D�ٴ��۵�ֽƬ��ʹ��C����ֱ��DB���ϣ��õ�C����ۺ�DE������OE����BD=t��
��1����t=1ʱ�����E�����ꣻ
��2����S�ı���OECB=s���ú�t��ʽ�ӱ�ʾs��Ҫ��д��t��ȡֵ��Χ����
��3����OEȡ��Сֵʱ�����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a5+a5=a10
B.a6��a4=a24
C.a0��a��1=a
D.a4��a4=a0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D��E��F�ֱ���BC��AB��AC���ϣ���BE=CF��AD+EC=AB�� 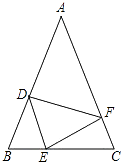
��1����֤����DEF�ǵ��������Σ�
��2������A=40��ʱ�����DEF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A.x3+x2��x5B.x3x2��x6
C.����x3��2��x5��1D.����x��3������x��2����x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߶�AB�Ƶ�O˳ʱ����ת90��õ��߶�A��B�䣬��ôA����2��5���Ķ�Ӧ��A��������ǣ� ��
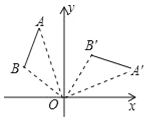
A����2��5�� B����5��2�� C����2����5�� D����5����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���Ӧ�ã��Ķ�1��a��bΪʵ������a��0��b��0����Ϊ![]() ������
������![]() �Ӷ�
�Ӷ�![]() ����a=bʱȡ�Ⱥţ���
����a=bʱȡ�Ⱥţ���
�Ķ�2��������![]() ����m��0��x��0��mΪ�����������Ķ�1���ۿ�֪��
����m��0��x��0��mΪ�����������Ķ�1���ۿ�֪��![]() �����Ե�
�����Ե�![]() ����
����![]() ʱ������
ʱ������![]() ����СֵΪ
����СֵΪ![]() ��
��
�Ķ������������ݣ�����������⣺
����1����֪һ�����ε����Ϊ4������һ�߳�Ϊx������һ�߳�Ϊ![]() ���ܳ�Ϊ2��
���ܳ�Ϊ2��![]() ������x= ʱ���ܳ�����СֵΪ ��
������x= ʱ���ܳ�����СֵΪ ��
����2����֪����![]() ��
��![]() ���뺯��
���뺯��![]() ��
��![]() ����
����
��x= ʱ��![]() ����СֵΪ ��
����СֵΪ ��
����3��ij���ѧУÿ���֧���ܷ��ð��������������֣�һ�ǽ�ְ������4900Ԫ������ѧ������ѳɱ�ÿ��10Ԫ�������������ã����У�����������ѧ��������ƽ�������ȣ�����ϵ��Ϊ0.01����ѧУѧ������Ϊ����ʱ����Уÿ������Ͷ����ͣ���ͷ����Ƕ���Ԫ��������Ͷ��=֧���ܷ��á�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��CB��AB��CEƽ�֡�BCD��DEƽ�֡�CDA����1+��2=90�㣬��֤��DA��AB��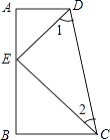
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com