
【题目】如图,ABCD的顶点A,B的坐标分别是A(﹣1,0),B(0,﹣3),顶点C,D在双曲线y= ![]() 上,边AD交y轴于点E,且ABCD的面积是△ABE面积的8倍,则k= .
上,边AD交y轴于点E,且ABCD的面积是△ABE面积的8倍,则k= . 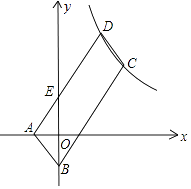
【答案】36
【解析】解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H, ∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=3,设C(m+1,n),D(m,n+3),
则(m+1)n=m(n+3)=k,
解得n=3m,则D的坐标是(m,3m+3),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得![]() ,
,
由①得:a=b,代入②得:mb+b=3m+3,
即b(m+1)=3(m+1),解得b=3,
则 ![]() ,
,
∴y=3x+3,E(0,3),BE=6,
∴S△ABE= ![]() ×BE×AO=3,
×BE×AO=3,
∵S四边形ABCD=8S△ABE=24,
∴S四边形ABCD=2S△ABE+S四边形BEDM=24,
即6+6×m=24,
解得m=3,
∴n=3m=9,
∴k=(m+1)n=4×9=36.
所以答案是:36.
【考点精析】通过灵活运用比例系数k的几何意义和平行四边形的性质,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) 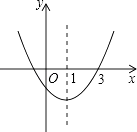
A.abc<0
B.4ac﹣b2<0
C.a﹣b+c<0
D.2a+b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
数学活动课上,老师出了一道作图问题:“如图,已知直线l和直线l外一点P.用直尺和圆规作直线PQ,使PQ⊥l于点Q.”

小艾的作法如下:
(1)在直线l上任取点A,以A为圆心,AP长为半径画弧.
(2)在直线l上任取点B,以B为圆心,BP长为半径画弧.
(3)两弧分别交于点P和点M
(4)连接PM,与直线l交于点Q,直线PQ即为所求.
老师表扬了小艾的作法是对的.
请回答:小艾这样作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.
求作:菱形AMBN,使得其对角线分别等于b和2a.
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.
求作:菱形AMBN,使得其对角线分别等于b和2a.
小军的作法如下:
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于![]() AB的长为半径,
AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于![]() AB的长为半径,
AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
老师说:“小军的作法正确.”
该上面尺规作图作出菱形AMBN的依据是_______________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.
已知:如图,钝角∠AOB.
求作:∠AOB的角平分线.
作法:
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() DE的长为半径作弧,在∠AOB内,两弧交于点C;
DE的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
请回答:该尺规作图的依据是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
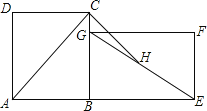
【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com