
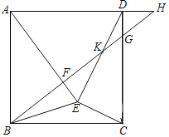
【题目】如图,在边长为4正方形ABCD中,以AB为腰向正方形内部作等腰△ABE,点G在CD上,且CG=3DG.连接BG并延长,与AE交于点F,与AD延长线交于点H.连接DE交BH于点K.若AE2=BFBH,则S△CDE=__.
【答案】![]()
【解析】
根据题意作EM⊥AB于M,EM交CD于N,如图,利用勾股定理计算出BG=5,再证明△HDG∽△HAB,利用相似比计算出HB=![]() ,再证明△BAF∽△BHA得到∠BFA=∠BAH=90°,接着求出BF得到ME=BF=
,再证明△BAF∽△BHA得到∠BFA=∠BAH=90°,接着求出BF得到ME=BF=![]() ,然后计算出EN后利用三角形面积公式计算.
,然后计算出EN后利用三角形面积公式计算.
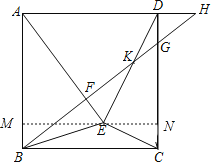
解:作EM⊥AB于M,EM交CD于N,如图,则EN⊥CD,
∵CG=3DG,
∴DG=1,CG=3,
在Rt△BCG中,BG=![]() =5,
=5,
∵DG∥AB,
∴△HDG∽△HAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得HB=
,解得HB=![]() ,
,
∵AE2=BFBH,而AB=AE,
∴AB2=BFBH,即AB:BF=BH:AB,
而∠ABF=∠HBA,
∴△BAF∽△BHA,
∴∠BFA=∠BAH=90°,
∴BF⊥EM,
∵BF=![]() =
=![]() ,
,
∴ME=BF=![]() ,
,
∴EN=4﹣![]() =
=![]() ,
,
∴S△CDE=![]() ×4×
×4×![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为 ;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字与十位数字之和为8,且千位数字a使得二次函数y=(a﹣2)x2﹣(2a﹣3)x+a﹣3与x轴有两个交点,求出所有满足条件的“平衡数”M的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
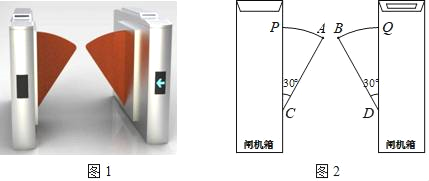
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
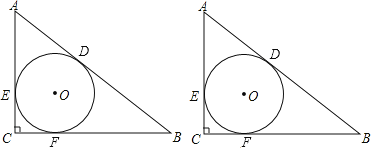
(1)若AC=3,BC=4,求△ABC的内切圆半径;
(2)当AD=5,BD=7时,求△ABC的面积;
(3)当AD=m,BD=n时,直接写出求△ABC的面积(用含m,n的式子表示)为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
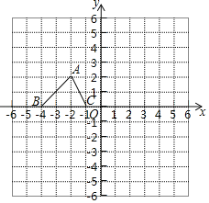
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣4,0)、C(﹣1,0).
(1)请直接写出点A关于y轴对称的点D的坐标;
(2)将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1并求点A在这一旋转中经过的路程.
(3)将△ABC以点C为位似中心,放大2倍得到△A2B2C,请写出一个点A2的坐标并画出△A2B2C.(所画图形必须在所给的网格内)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+3的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△APC的面积为5,求点P的坐标;
(3)直接写出不等式﹣x+3<![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点D,E分别在BC,AC上,且DC=AE,AD与BE交于点P,连接PC.
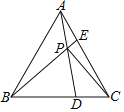
(1)证明:ΔABE≌ΔCAD.
(2)若CE=CP,求证∠CPD=∠PBD.
(3)在(2)的条件下,证明:点D是BC的黄金分割点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com