
【题目】如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB,CD边于点E,F.
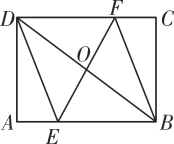
(1)求证:四边形DEBF是平行四边形;
(2)当DE=DF时,求EF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由矩形的性质得到AB∥CD,再根据平行线的性质得到∠DFO=∠BEO再证明△DOF≌△BOE,根据全等三角形的性质得到DF=BE,从而得到四边形BEDF是平行四边形;
(2)先证明四边形BEDF是菱形,再得到DE=BE,EF⊥BD,OE=OF,设AE=x,则DE=BE=8-x根据勾股定理求解即可.
(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DFO=∠BEO.
在△DOF和△BOE中
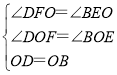 ,
,
∴△DOF≌△BOE(AAS).
∴DF=BE.
又∵DF∥BE,∴四边形BEDF是平行四边形.
(2)解:∵DE=DF,四边形BEDF是平行四边形,
∴四边形BEDF是菱形.
∴DE=BE,EF⊥BD,OE=OF.
设AE=x,则DE=BE=8-x,
在Rt△ADE中,根据勾股定理,有AE2+AD2=DE2,
∴x2+62=(8-x)2.解得x=![]() .
.
∴DE=8-![]() =
=![]() .
.
在Rt△ABD中,根据勾股定理,有AB2+AD2=BD2,
∴BD=![]() =10.
=10.
∴OD=![]() BD=5.
BD=5.
在Rt△DOE中,根据勾股定理,有DE2-OD2=OE2,
∴OE=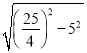 =
=![]() .
.
∴EF=2OE=![]() .
.


科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,按如图方式作正方形
,按如图方式作正方形![]() 、
、![]() 、
、![]() ,点
,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 在
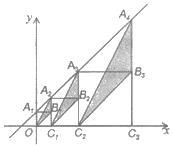
在![]() 轴上,图中阴影部分三角形的面积从左到右依次记为
轴上,图中阴影部分三角形的面积从左到右依次记为![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“半日走遍江淮大地,安徽风景尽在徽园”,位于省会合肥的徽园景点某年三月共接待游客![]() 万人,四月比三月旅游人数增加了
万人,四月比三月旅游人数增加了![]() ,五月比四月游客人数增加了
,五月比四月游客人数增加了![]() ,已知三月至五月徽园的游客人数平均月增长率为
,已知三月至五月徽园的游客人数平均月增长率为![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片![]() 和
和![]() 按图1所示放置,直角顶点重合在点
按图1所示放置,直角顶点重合在点![]() 处,
处,![]() ,
,![]() .保持纸片
.保持纸片![]() 不动,将纸片
不动,将纸片![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]()
![]() .当
.当![]() 与
与![]() 在同一直线上(如图2)时,
在同一直线上(如图2)时,![]() 的正切值等于_________.
的正切值等于_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形上存在点
,如果在图形上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对“倍点”.已知⊙O的半径为
的一对“倍点”.已知⊙O的半径为![]() ,点
,点![]() .
.
(1)①点![]() 到⊙O的最大值是_______,最小值是_______;
到⊙O的最大值是_______,最小值是_______;
②在![]() ,
,![]() ,这两个点中,与点
,这两个点中,与点![]() 是⊙O的一对“倍点”的是_______;
是⊙O的一对“倍点”的是_______;
(2)在直线![]() 上存在点
上存在点![]() 与点
与点![]() 是⊙O的一对“倍点”,求
是⊙O的一对“倍点”,求![]() 的取值范围;
的取值范围;
(3)已知直线![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点的
轴分别交于点的![]() ,
,![]() ,若线段
,若线段![]() (含端点
(含端点![]() ,
,![]() )上所有点与点
)上所有点与点![]() 都是⊙O的一对“倍点”,直接写出
都是⊙O的一对“倍点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
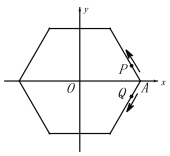
【题目】如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A.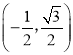 B.
B.![]() C.
C.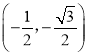 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
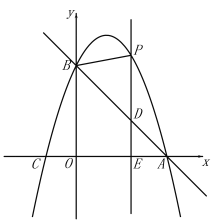
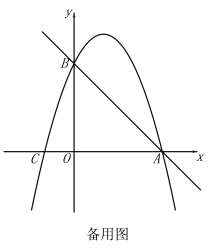
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
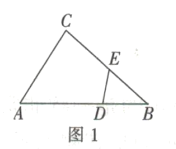
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
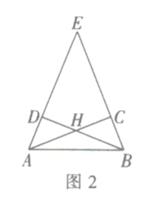
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
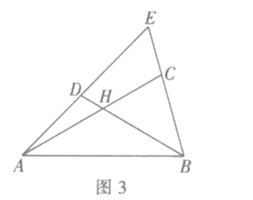
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,![]() 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
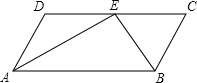
【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com