
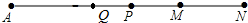
分析 根据线段中点的定义可知:AP=$\frac{1}{2}(AM+MN)$、AQ=$\frac{1}{2}$AM,故QP=AP-AQ=$\frac{1}{2}MN$,然后代入求解即可.
解答 解:∵P是AN的中点,
∴AP=$\frac{1}{2}$AN=$\frac{1}{2}(AM+MN)$.
∵Q是AM的中点,
∴AQ=$\frac{1}{2}$AM.
∴QP=AP-AQ=$\frac{1}{2}(AM+MN)$-$\frac{1}{2}$AM=$\frac{1}{2}MN$.
∴MN:PQ=MN:$\frac{1}{2}$MN=2.
点评 本题主要考查的是两点间的距离,依据线段中点的定义以及线段的和差关系得到PQ=$\frac{1}{2}MN$是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com