
【题目】已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,AB=![]() ,sinB=
,sinB=![]() ,反比例函数
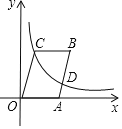
,反比例函数![]() 的图象经过点C以及边AB的中点D,则四边形OABC的面积为_____.
的图象经过点C以及边AB的中点D,则四边形OABC的面积为_____.
【答案】12
【解析】
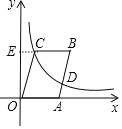
延长BC交y轴于E,如图,利用平行四边形的性质得BC=OA,BC∥OA,OC∥AB,OC=AB=2![]() ,在Rt△OCE中利用解直角三角形计算出OE=4,CE=2,从而得到C(2,4),设B(t+2,4),则D(t+1,2),根据反比例函数图象上点的坐标特征得到2(t+1)=2×4,然后求出t后利用平行四边形的面积公式计算四边形OABC的面积.
,在Rt△OCE中利用解直角三角形计算出OE=4,CE=2,从而得到C(2,4),设B(t+2,4),则D(t+1,2),根据反比例函数图象上点的坐标特征得到2(t+1)=2×4,然后求出t后利用平行四边形的面积公式计算四边形OABC的面积.
解:延长BC交y轴于E,如图,
∵四边形OABC为平行四边形,
∴BC=OA,BC∥OA,OC∥AB,OC=AB=2![]() ,
,
∴BE⊥y轴,∠OCE=∠B,
在Rt△OCE中,sin∠OCE=![]() =sinB=
=sinB=![]() ,
,
∴OE=![]() ×2
×2![]() =4,
=4,
∴CE=![]() =2,
=2,
∴C(2,4),
设B(t+2,4),
∵D点为AB的中点,
∴D(t+1,2),
∵点C、D在反比例函数y=![]() 的图象上,
的图象上,
∴2(t+1)=2×4,解得t=3,
∴BC=4,
∴四边形OABC的面积=3×4=12.
故答案为12.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
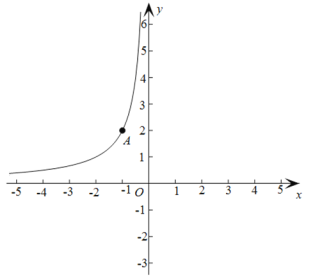
【题目】已知:在平面直角坐标系xOy中,点A(-1,2)在函数![]() (x<0)的图象上.
(x<0)的图象上.
(1)求m的值;
(2)过点A作y轴的平行线![]() ,直线
,直线![]() 与直线
与直线![]() 交于点B,与函数
交于点B,与函数![]() (x<0)的图象交于点C,与
(x<0)的图象交于点C,与![]() 轴交于点D.
轴交于点D.
①当点C是线段BD的中点时,求b的值;
②当BC<BD时,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
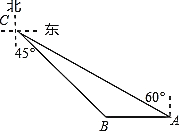
【题目】如图,码头![]() 在码头
在码头![]() 的正东方向,两个码头之间的距离为10海里,今有一货船由码头
的正东方向,两个码头之间的距离为10海里,今有一货船由码头![]() 出发,沿北偏西60°方向航行到达小岛
出发,沿北偏西60°方向航行到达小岛![]() 处,此时测得码头
处,此时测得码头![]() 在南偏东45°方向,则码头
在南偏东45°方向,则码头![]() 与小岛
与小岛![]() 的距离为_________海里(结果保留根号).
的距离为_________海里(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学疫情期间为了切实抓好“停课不停学”活动,借助某软件平台随机抽取了该校部分学生的在线学习时间,并将结果绘制成如下两幅不完整的统计图.

请你根据以上信息回答下列问题
(1)本次调查的人数为 , 学习时间为7小时的所对的圆心角为 ;
(2)补全频数分布直方图;
(3)若全校共有学生1800人,估计有多少学生在线学习时间不低于8个小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过点B(1,0)的抛物线![]() 与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
与y轴交于点C,其顶点为点G,过点C作y轴的垂线交抛物线对称轴于点D,线段CO上有一动点M,连接DM、DG.
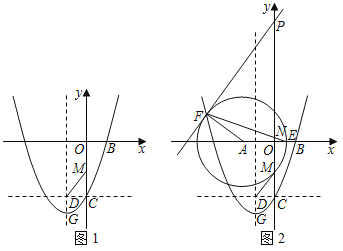
(1)求抛物线的表达式;
(2)求![]() 的最小值以及相应的点M的坐标;
的最小值以及相应的点M的坐标;
(3)如图2,在(2)的条件下,以点A(﹣2,0)为圆心,以AM长为半径作圆交x轴正半轴于点E.在y轴正半轴上有一动点P,直线PF与⊙A相切于点F,连接EF交y轴于点N,当PF∥BM时,求PN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为△ABC边AB上的一点,⊙O为△BCE的外接圆,点D为![]() 上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
(1)求证:∠CAE+∠CDE=90°;
(2)①如图2,当CD过圆心O时,①将△ACD绕点A顺时针旋转得△AEF,连接DF,请补全图形,猜想CD、DE、DF之间的数量关系,并证明你的猜想;②若n=3,求AD的长.

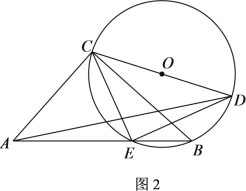
查看答案和解析>>
科目:初中数学 来源: 题型:
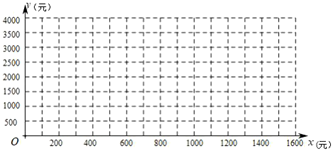
【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费![]() ,
,![]() (元)与印制数量
(元)与印制数量![]() (份)之间的关系式(不用写出自变量的取值范围);
(份)之间的关系式(不用写出自变量的取值范围);
(2)在同一坐标系内画出它们的图象,并求出当印制多少份宣传材料,两个印刷厂的印制费用相同?此时费用为多少?
(3)结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印制省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为_____.
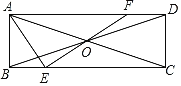
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com