练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

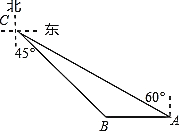
    【题目】如图，码头在码头的正东方向，两个码头之间的距离为10海里，今有一货船由码头出发，沿北偏西60°方向航行到达小岛处，此时测得码头在南偏东45°方向，则码头与小岛的距离为_________海里（结果保留根号）.

    【答案】

    【解析】

    在Rt△DCB中，可得CD的长，在Rt△CAD中，由30°角所对直角边等于斜边的一边，可得答案．

    作CD⊥AB交AB延长线于点D，∠D=90°，如图，

    由题意，得∠DCB=45°，∠CAD=90°﹣60°=30°，AB=10海里，

    设CD=x海里，

    在Rt△DCB中，tan∠DCB=，tan45°==1，BD=x，AD=AB+BD=10+x，

    tan30°=，解得x=，

    ∵∠CAD=30°，∠CDA=90°，∴AC=2CD=（海里），

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】事业单位人员编制连进必考，现一事业单位需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表：

    笔试

    面试

    体能

    甲

    84

    80

    88

    乙

    94

    92

    69

    丙

    81

    84

    78

    （1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序；

    （2）该单位规定：笔试、面试、体能分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分.根据规定，请你说明谁将被录用.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

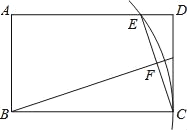
    【题目】如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，连接CE，作BF⊥CE，垂足为F，则tan∠FBC的值为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

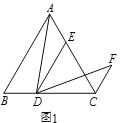
    【题目】(1)问题发现：如图1，在等边中，点为边上一动点，交于点，将绕点顺时针旋转得到，连接．则与的数量关系是_____，的度数为______．

    (2)拓展探究：如图2，在中，，，点为边上一动点，交于点，当∠ADF=∠ACF=90°时，求的值．

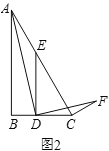
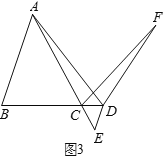
    (3)解决问题：如图3，在中，，点为的延长线上一点，过点作交的延长线于点，直接写出当时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市用1200元购进一批甲玩具，用800元购进一批乙玩具，所购甲玩具件数是乙玩具件数的，已知甲玩具的进货单价比乙玩具的进货单价多1元．

    （1）求：甲、乙玩具的进货单价各是多少元？

    （2）玩具售完后，超市决定再次购进甲、乙玩具（甲、乙玩具的进货单价不变），购进乙玩具的件数比甲玩具件数的2倍多60件，求：该超市用不超过2100元最多可以采购甲玩具多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】每年的3月15日是“国际消费者权益日”，许多家居商城都会利用这个契机进行打折促销活动.甲卖家的某款沙发每套成本为5000元，在标价8000元的基础上打9折销售.

    （1）现在甲卖家欲继续降价吸引买主，问最多降价多少元，才能使利润率不低于20%？

    （2）据媒体爆料，有一些卖家先提高商品价格后再降价促销，存在欺诈行为.乙卖家也销售相同的沙发，其成本、标价与甲卖家一致，以前每周可售出8套，现乙卖家先将标价提高，再大幅降价元，使得这款沙发在3月15日那一天卖出的数量就比原来一周卖出的数量增加了，这样一天的利润达到了50000元，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

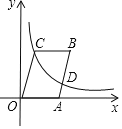
    【题目】已知：如图，直线交坐标轴于A、C两点，抛物线过A、C两点．

    （1）求抛物线的解析式；

    （2）若点P为抛物线位于第三象限上一动点，连接PA，PC，试问△PAC是否存在最大值，若存在，请求出△APC取最大值以及点P的坐标，若不存在，请说明理由；

    （3）点M为抛物线上一点，点N为抛物线对称轴上一点，若△NMC是以∠NMC为直角的等腰直角三角形，请直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平面直角坐标系xOy中，点A在x轴的正半轴上，点B、C在第一象限，且四边形OABC是平行四边形，AB＝，sinB＝，反比例函数的图象经过点C以及边AB的中点D，则四边形OABC的面积为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E．将△BDE沿直线DE折叠，得到△B′DE，若B′D，B′E分别交AC于点F，G，连接OF，OG，则下列判断错误的是（　　）

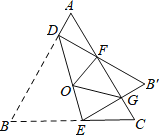
    A. △ADF≌△CGE

    B. △B′FG的周长是一个定值

    C. 四边形FOEC的面积是一个定值

    D. 四边形OGB'F的面积是一个定值

    查看答案和解析>>

    同步练习册答案