
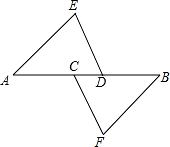
如图:点 C、D 在 AB 上,且 AC=BD,AE=FB,DE=FC.求证:AE∥BF.
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
如图,己知线段 AB=12 厘米,动点 P 以 2 厘米/秒的速度从点 A 出发向点 B 运动,动点 Q 以 4 厘米/秒的速度从点 B 出发向点 A 运动.两点同时出发,到达各自的终点后停止运动.设两点之 间的 距离为 s(厘米),动点 P 的运动时间为 t 秒,则下图中能正确反映 s 与 t 之间的函数关系的是( )
间的 距离为 s(厘米),动点 P 的运动时间为 t 秒,则下图中能正确反映 s 与 t 之间的函数关系的是( )
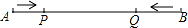
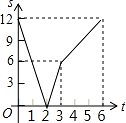
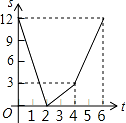 A.
A. 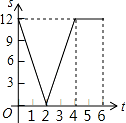 B.
B. 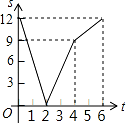 C.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= 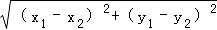 .
.
 例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=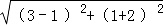 = .
= .
特别地,如果两 点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com