练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，AB=AC，D是AB的中点，且DE⊥AB于点D，AB=10，BC=4，则△BEC的周长(     )

    A．14     B．6       C．9       D．12


    A【考点】线段垂直平分线的性质；等腰三角形的性质．

    【分析】根据线段垂直平分线性质得出AE=BE，求出三角形BEC的周长=AC+BC，代入求出即可．

    【解答】解：∵D是AB的中点，DE⊥AB，

    ∴AE=BE，

    ∵AB=AC=10，BC=4，

    ∴△BEC的周长是BC+BE+CE=BC+AE+CE=BC+AC=4+10=14，

    故选A．

    【点评】本题考查了线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    设x1，x2是方程x2﹣x﹣1=0的两个根，则代数式x13+2x2+x1•x2的值为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    命题：①邻补角互补；②对顶角相等；③同旁内角互补；④两点之间线段最短；⑤直线都相等．其中真命题有(     )

    A．1个  B．2个  C．3个  D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一根弹簧的原长是10 cm，且每挂重1kg就伸长0.5 cm，它的挂重不超过10kg．

    （1）挂重后弹簧的长度y（cm）与挂重x（kg）之间的函数关系式；

    （2）写出自变量的取值范围；

    （3）挂重多少千克时，弹簧长度为12.5cm？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若用同一种正多边形瓷砖铺地面，能铺满地面的正多边形是(     )

    A．正五边形 B．正六边形  C．正七边形 D．正八边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=5，则AC=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．求证：

    （1）△ABD≌△ACD；

    （2）BE=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形a，b，c，d，e，f的面积和为32，则最大的正方形ABCD的边长为__________．

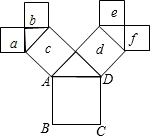
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中和△DEF中，已知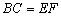，∠C=∠F，增加下列条件后还不能判定△ABC≌△DEF的是（   ）wwA．AC=DF ；   B．AB=DE；      C．∠A=∠D ；   D．∠B=∠E；

    查看答案和解析>>

    同步练习册答案