
【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,过点
上,过点![]() 作
作![]() 的平行线
的平行线![]() ,如果
,如果![]() ,那么
,那么![]() 的度数为__________.
的度数为__________.

【答案】(1)①中线;②是;(2)见解析;(3)![]() .
.
【解析】
(1)①根据中线及二分线的定义即可求解;
②先由AD是BC边上的中线可得S△ABD=S△ACD,再根据![]() 可得S四边形ACFE=S△BEF即可求解;
可得S四边形ACFE=S△BEF即可求解;
(2)先证△CDG≌△EAG可得S△CDG=S△EAG,再根据F是EB的中点即可求解;
(3)分别证明△AEB≌△CDE,△AEB≌△EBH,△MHB≌△MAE,然后得出S△MHB=S△MAE,再根据全等三角形的性质及二分线定义即可求解.
(1)①三角形的中线、高线、角平分线中,一定是三角形的二分线的是中线,
故答案为中线;
②∵AD是BC边上的中线,
∴S△ABD=S△ACD,
又∵![]() ,
,
∴S四边形BEGD=S四边形AGFC,
∴S四边形BEGD+![]() =S四边形AGFC+
=S四边形AGFC+![]() ,
,
∴![]() =S四边形AEFC,
=S四边形AEFC,
所以EF是△ABC的一条二分线,故答案为是;
(2)∵点G是AD的中点,
∴GD=AG,
∵AB∥DC,
∴∠D=∠GAE,
在△CDG和△EAG中,
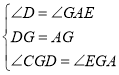 ,
,
∴△CDG≌△EAG(ASA),
∴S△CDG=S△EAG,
∵点F是EB的中点,
∴S△CFE=S△CBF,
即S△AGE+S四边形AGCF=S△CBF,
∴S△CDG+S四边形AGCF=S△CBF,即S四边形ADCF=S△CBF,
∴CF是四边形ABCD的二分线;
(3)如图,延长CB于点H,使得BH=AE,连接EH交AB于点M,
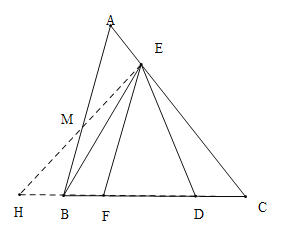 ,
,
∵AB=BC,
∴∠A=∠C,
∵∠BED=∠A,
∴∠AEB=∠CDE,
在△AEB和△CDE中,
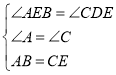 ,
,
∴△AEB≌△CDE(AAS),
∴AE=CD,
∴BH=CD,
∴DH=CB,
∵CB=CE,
∴∠CBE=∠CEB,
∴∠HBE=∠AEB,
在△EBH和△BEA中,
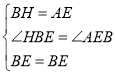 ,
,
∴△AEB≌△EBH(SAS),
∴∠H=∠A,
在△MBH和△MEA中,
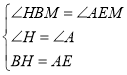 ,
,
∴△MHB≌△MAE(ASA),
∴S△MHB=S△MAE,
∴S△HMB+S四边形MBFE=S△AME+S四边形MBFE,即S△HEF=S四边形ABFE,
∵EF是四边形ABDE的一条二分线,
∴S四边形ABFE=S△DEF,
∴S△HEF=S△DEF,
∴DF=![]() DH=
DH=![]() CB=
CB=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() (
(![]() 为常数).
为常数).
(1)求这个二元一次方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,设
,设![]() ,且m为正整数,求m的值.
,且m为正整数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE等于 _________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道:截止到2013年12月31日我国微信用户规模已达到6亿.以下是根据相关数据制作的统计图表的一部分:
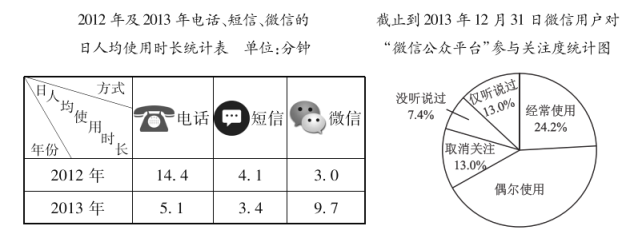
请根据以上信息,回答以下问题:
(1)从2012年到2013年微信的日人均使用时长增加了 分钟;
(2)截止到2013年12月31日,在我国6亿微信用户中偶尔使用微信用户约为 亿(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
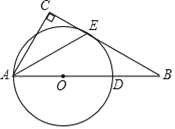
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点,△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).(提示:有一个角是60°的等腰三角形是等边三角形)
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO. ③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
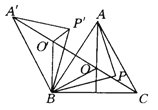
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com