
已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内, △ABC的三个顶点坐标分别为A(2,-4), B(4,-4),C(1,-1).
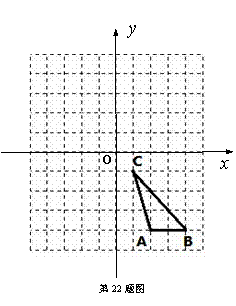
(1)画出△ABC关于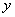 轴对称的△A1B1C1,直接写出点A1的坐标____________.
轴对称的△A1B1C1,直接写出点A1的坐标____________.
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2.
 (3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
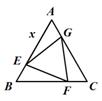
如题10图,已知正△ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设 △EFG的面积为y,AE的长为x,则y关于x的函数图象大致是

查看答案和解析>>
科目:初中数学 来源: 题型:
某学校小组5名同学的身高(单位:cm)分别为:147,151,152,156,159,则这组数据的中位数是( )
A. 147 B. 151 C. 152 D. 156
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com