
分析 首先根据幂的乘方的运算方法,可得8n=(23)n=23n,16n=(24)n=24n,然后根据2×8n×16n=225,可得21+3n+4n=225,据此求出n的值是多少即可.
解答 解:∵2×8n×16n=225,
∴2×23n×24n=225,
∴21+3n+4n=225,
∴21+7n=225,
∴1+7n=25,
解得n=3$\frac{3}{7}$,
∴n的值是3$\frac{3}{7}$.
故答案为:3$\frac{3}{7}$.
点评 (1)此题主要考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).
(2)此题还考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | -(-2x+3)=2x-3 | B. | -(2x-3)=2x+3 | C. | -(-2x-3)=-2x+3 | D. | -(2x+3)=-2x+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成本P(元/kg) | 8-$\frac{x}{10}$ |
| 销售量q(kg) | 1000-10x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
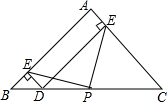 如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.
如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
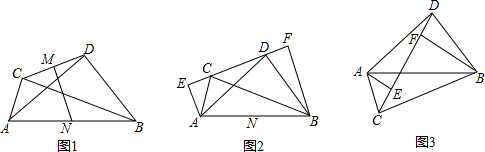
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
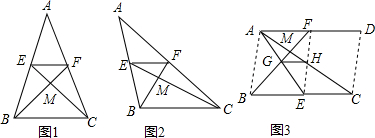
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com