
| 成本P(元/kg) | 8-$\frac{x}{10}$ |
| 销售量q(kg) | 1000-10x |
分析 (1)将售价减去第x天水果的成本可得;
(2)把y=($\frac{x}{10}$+7)q=-x2+30x+7000,配方得到y=-(x-15)2+7225,即可得到结论;
(3)根据题意得到y═($\frac{x}{10}$+7-m)q=-[x-(15+5m)]2+7225+25m2-850m,由于对称轴x=15+5m≥20,解得m≥1,于是得到结论.
解答 解:(1)根据题意,第x天水果的成本为(8-$\frac{x}{10}$)元/kg,其售价为15元/千克,
故第x天每销售1kg水果获得的利润为:15-(8-$\frac{x}{10}$)=7+$\frac{x}{10}$;
(2)y=(7+$\frac{x}{10}$)(1000-10x)
=-x2+30x+7000,
=-(x-15)2+7225,
所以当x=15时,y取得最大值,最大值为7225,
答:第15天的利润最大,最大利润为:7225元;
(3)y═($\frac{x}{10}$+7-m)(1000-10x)=-[x-(15+5m)]2+7225+25m2-850m,
∵对称轴x=15+5m≥20,
∴m≥1,
∴m的取值范围:1≤m≤2.
点评 本题考查了二次函数的应用,熟知利润=每千克的利润×销量是关键,求m的取值范围时要求对二次函数的增减性灵活掌握.


科目:初中数学 来源: 题型:解答题
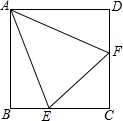 在正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为长为x
在正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF的面积为y,EC为长为x查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=BC,AD=DC | B. | AB∥CD,AD=CB | C. | OA=OC,OB=OD | D. | AC=BD,AC⊥BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2x-3=5变形为-2x=5+3 | B. | 2(x-1)=-4变形为2x-2=-4 | ||
| C. | $\frac{x}{2}$+1=$\frac{x-1}{3}$变形为 3x+6=2(x-1) | D. | -2x=6变形为x=-$\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com