
分析 (1)根据配方法解方程即可;
(2)根据因式分解法求解即可;
(3)根据直接开平方法解一元二次方程即可;
(4)把2x-1看作整体,利用因式分解法解方程即可.
解答 解:(1)x2+2x=2,
x2+2x+1=3,
(x+1)2=3,
x+1=±$\sqrt{3}$,
x1=$\sqrt{3}$-1,x2=-$\sqrt{3}$-1;
(2)x2-7x+10=0,
(x-2)(x-5)=0,
x-2=0,x-5-0,
x1=2,x2=5;
(3)(4x-1)2=27,
4x-1=±3$\sqrt{3}$,
x1=$\frac{3\sqrt{3}+1}{4}$,x2=$\frac{-3\sqrt{3}+1}{4}$;
(4)(2x-1)2-4(2x-1)=12
(2x-1-6)(2x-1+2)=0
2x-7=0或2x+1=0,
x1=$\frac{7}{2}$,x2=-$\frac{1}{2}$.
点评 本题考查了一元二次方程的解法,掌握解一元二次方程的方法:配方法、公式法、因式分解法是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
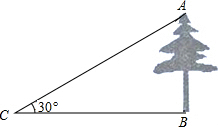 如图所示,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为30°,BC=40m,求树的高度AB.(计算过程和结果均不取近似值)
如图所示,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为30°,BC=40m,求树的高度AB.(计算过程和结果均不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{1}{3}$ | B. | x≥$\frac{1}{3}$ | C. | x>2 | D. | $\frac{1}{3}$≤x<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com