
如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(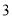 ,
, ),与y轴交于C(
),与y轴交于C( ,
, )点,点P是直线BC下方的抛物线上一动点.
)点,点P是直线BC下方的抛物线上一动点.

(1)求这个二次函数的解析式;
(2)若抛物线的顶点为点D,求△BCD的面积;
(3)设M是(1)所得抛物线上第四象限内的一个动点,过点M作直线l⊥x 轴于点F,交直线BC于点N。试问:线段MN的长度是否存在最大值?若存在,求出它最大值及此时M点的坐标;若不存在,请说明理由.
(1)y=x2﹣2x﹣3;(2)3;(3) 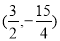
【解析】
试题分析:(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值;(2)过点D作DE⊥y轴于点E,则∠DEC=∠BOC=90°根据B(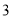 ,
,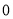 ),C(
),C(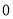 ,
,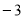 )可得OB=3,OC=3 把y=x2﹣2x﹣3 配方的为:
)可得OB=3,OC=3 把y=x2﹣2x﹣3 配方的为: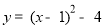 求出顶点D(1,-4),所以可得OE=4,DE=1 ,CE=OE-OC=4-3=1,从而求出△BCD的面积
求出顶点D(1,-4),所以可得OE=4,DE=1 ,CE=OE-OC=4-3=1,从而求出△BCD的面积
(3)设直线BC的关系式为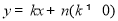 ,将 B(
,将 B(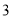 ,
,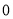 ),C(
),C(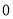 ,
,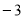 )带入
)带入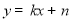 中,求得直线DE的关系式为
中,求得直线DE的关系式为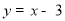 ,根据点M在抛物线上,点N在直线BC上,MN⊥x 轴于点F,M、N在第四象,求出线段MN长度有最大值即可求出此时M点的坐标
,根据点M在抛物线上,点N在直线BC上,MN⊥x 轴于点F,M、N在第四象,求出线段MN长度有最大值即可求出此时M点的坐标
试题解析:【解析】
(1)将B(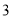 ,
,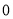 ),C(
),C(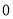 ,
,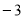 )两点的坐标代入得 :
)两点的坐标代入得 :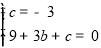
解得:b=-2,c=-3;
所以二次函数的表达式为:y=x2﹣2x﹣3
(2)过点D作DE⊥y轴于点E,则∠DEC=∠BOC=90°
∵B(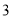 ,
,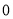 ),C(
),C(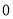 ,
,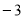 )∴OB=3,OC=3
)∴OB=3,OC=3
y=x2﹣2x﹣3 配方的: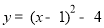
∴D(1,-4)
∴OE=4,DE=1 ∴CE=OE-OC=4-3=1
∴ 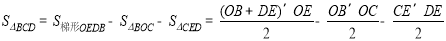
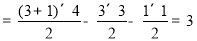 .
.
(3)设直线BC的关系式为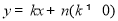
将 B(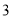 ,
,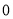 ),C(
),C(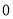 ,
,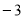 )带入
)带入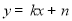 中
中
则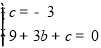
解得k=1,n=-3
∴直线DE的关系式为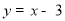
∵点M在抛物线上,点N在直线BC上
又∵MN⊥x 轴于点F,M、N在第四象限
∴设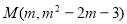 、
、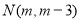
∴MF=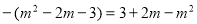 ,NF=
,NF=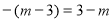
∴MN=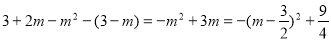
∴当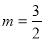 时,线段MN长度有最大值为
时,线段MN长度有最大值为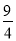 ,此时M的坐标为
,此时M的坐标为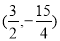
考点:1.待定系数法二次函数解析式的确定;2二次函数的性质;3.图形面积的求法


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:2014-2015学年重庆市等九年级模拟联考数学试卷(解析版) 题型:选择题
已知⊙O的直径为8cm,圆心O到直线AB的距离为5cm,则⊙O与直线AB的位置关系是( )
A.相交 B.相切 C.相离 D.外离
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市沙坪坝区九年级上学期期中联考数学试卷(解析版) 题型:解答题
某中学九(1)班为了了解全班学生喜欢球类活动的情况,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),
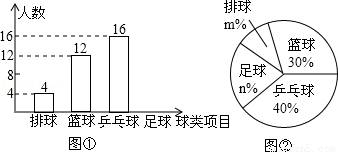
请你根据图中提供的信息解答下列问题:各个兴趣小组人数统计图各个兴趣小组总人数占调查人数百分比统计图
(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市校七年级12月月考数学试卷(解析版) 题型:选择题
如图所示,关于线段、射线和直线的条数,下列说法正确的是( )

A.五条线段,三条射线
B.一条直线,三条线段
C.三条线段,两条射线,一条直线
D.三条线段,三条射线
查看答案和解析>>
科目:初中数学 来源:2014-2015山东省威海市环翠区七年级上学期期中考试数学试卷(解析版) 题型:选择题
一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
取3)是( )

A.20cm B.10cm C.14cm D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com