
【题目】如图,正方形网格中,每一个小正方形的边长都是1个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,1),B(3,2),C(2,4).
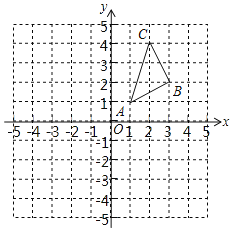
(1)画出△ABC关于x轴对称的△A1B1C1,直接写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求BC边所扫过的面积.(结果保留π)
【答案】(1)如图,△A1B1C1即为所求,见解析;点A1的坐标为:(1,﹣1);(2)△A2B2C2即为所求,见解析;(3)BC边所扫过的面积是![]() .
.
【解析】
(1)根据关于x轴对称的点的横坐标不变,纵坐标互为相反数,即可作出△ABC关于x轴对称的△A1B1C1,进而得出点A1的坐标;
(2)分别确定△ABC三个顶点绕点O逆时针旋转90°后的点,再连接即可得到△A2B2C2;
(3)先利用勾股定理解直角三角形,求得OB2和OC2,BC边所扫过的面积为S扇形OCC2-S扇形OBB2,利用扇形面积计算公式即可求解.
(1)如图,分别画出△ABC三个顶点A、B、C关于x轴对称的点A1、B1、C1,再连接点A1、B1、C1,△A1B1C1即为所求;
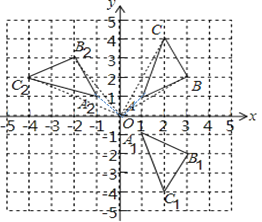
∵A(1,1),点A和A1关于x轴对称
∴点A1的坐标为:(1,﹣1)
故答案为:作图见解析,点A1的坐标为(1,﹣1)
(2)连接OA、OB、OC,将OA、OB、OC绕点O逆时针旋转90°后得到OA2、OB2、OC2,连接点A2、B2、C2,△A2B2C2即为所求;
(3)∵OB2=32+22=13,
OC2=42+22=20,
∴BC边所扫过的面积为:S扇形OCC2-S扇形OBB2=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
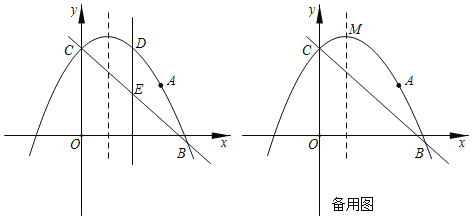
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价a元,则平均每天销售数量为 件.(用含a的代数式表示)
(2)当每件商品降价多少元时,该商店每天销售利润为1200元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BCA=90°,D为AC边上一动点,O为BD中点,DE⊥AB,垂足为E,连结OE,CO,延长CO交AB于F,设∠BAC=α,则( )
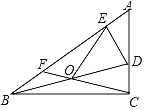
A.∠EOF=![]() αB.∠EOF=2α
αB.∠EOF=2α
C.∠EOF=180°﹣αD.∠EOF=180°﹣2α
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店销售口罩,进价15元,售价20元,为防控新冠肺炎疫情,药店决定凡是一次性购买10个以上的客户,每多买一个,售价就降低0.1元(顾客所购买的全部口罩),但最低价是17元/个.
(1)顾客一次性至少购买多少个口罩时,才能以最低价17元/个购买?
(2)写出一次性购买x个口罩时(x>10),药店的利润y(元)与购买量x(个)之间的函数关系式;
(3)在销售过程中,药店发现一次性卖出36个口罩时比卖出26个口罩的钱少,为了使每次销售均能达到多卖就能多获利,在其他促销条件不变的情况下,最低价应确定为每个多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:图①、图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点![]() 、点
、点![]() 和点
和点![]() 均在小正方形的顶点上.请在图①、图②中各画一个四边形,满足以下要求:
均在小正方形的顶点上.请在图①、图②中各画一个四边形,满足以下要求:

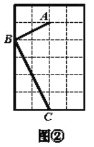
(1)在图①中以![]() 和
和![]() 为边画四边形
为边画四边形![]() ,点
,点![]() 在小正方形的顶点上,且此四边形四个内角中有一个角为45°;
在小正方形的顶点上,且此四边形四个内角中有一个角为45°;
(2)在图②中以![]() 和
和![]() 为边画四边形
为边画四边形![]() ,点
,点![]() 在小正方形的顶点上,且此四边形对角互补,并且四个内角中有一个角为钝角;
在小正方形的顶点上,且此四边形对角互补,并且四个内角中有一个角为钝角;
(3)请直接写出图②中![]() 的正切值.
的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y1=2kx+k与函数![]() ,定义新函数y=y2﹣y1
,定义新函数y=y2﹣y1
(1)若k=2,则新函数y= ;
(2)若新函数y的解析式为y=x2+bx﹣2,则k= ,b= ;
(3)设新函数y顶点为(m,n).
①当k为何值时,n有大值,并求出最大值;
②求n与m的函数解析式;
(4)请你探究:函数y1与新函数y分别经过定点B,A,函数![]() 的顶点为C,新函数y上存在一点D,使得以点A,B,C,D为顶点的四边形为平行四边形时,直接写出k的值.
的顶点为C,新函数y上存在一点D,使得以点A,B,C,D为顶点的四边形为平行四边形时,直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
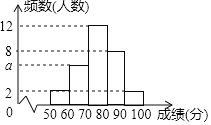
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为 ;
(2)若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为 度;
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有 人:
(4)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com