
【题目】在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证: 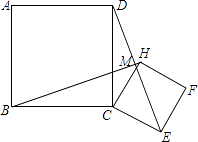
(1)BH=DE.
(2)BH⊥DE.
【答案】
(1)证明:在正方形ABCD与正方形CEFH中,
BC=CD,CE=CH,∠BCD=∠ECH=90°,
∴∠BCD+∠DCH=∠ECH+∠DCH,
即∠BCH=∠DCE,
在△BCH和△DCE中,
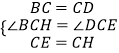 ,
,
∴△BCH≌△DCE(SAS),
∴BH=DE
(2)证明:∵△BCH≌△DCE,
∴∠CBH=∠CDE,
又∵∠CGB=∠MGD,
∴∠DMB=∠BCD=90°,
∴BH⊥DE.
【解析】(1)根据正方形的性质可得BC=CD,CE=CH,∠BCD=∠ECH=90°,然后求出∠BCH=∠DCE,再利用“边角边”证明△BCH和△DCE全等,根据全等三角形对应边相等证明即可;(2)根据全等三角形对应角相等可得∠CBH=∠CDE,然后根据三角形的内角和定理求出∠DMB=∠BCD=90°,再根据垂直的定义证明即可.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知点P(2-a,3a+6)到两坐标轴的距离相等,则点P的坐标为( )
A. (3,3) B. (6,-6) C. (3,3)或(6,-6) D. (3,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水资源保护组织对石家庄某小区的居民进行节约水资源的问卷调查.某居民在问卷上的选项代号画“√”,这个过程是收集数据中的( )
A.确定调查范围
B.汇总调查数据
C.实施调查
D.明确调查问题
查看答案和解析>>
科目:初中数学 来源: 题型:
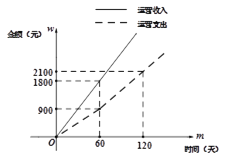
【题目】环保健康的“共享单车”已成为人们短途出行的一种新方式,一辆新投放市场的单车其先期成本为1050元. 如图是一辆新投放的共享单车其运营收入![]() 和运营支出
和运营支出![]() 关于时间
关于时间![]() 的函数图象。
的函数图象。
注:一辆单车的盈利=运营收入-运营支出-先期成本
(1)分别求![]() 及运营60天后
及运营60天后![]() 关于时间
关于时间![]() 的函数关系式.
的函数关系式.
(2)求一辆新投放市场的单车恰好收回先期成本需要运营多少天?
(3)某公司投放市场一批单车,其先期成本不少于2.1万元但不超过10.5万元,经过一段时间的市场试运营共盈利3550元,则该公司试运营的天数为 天(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是必然事件的是( )
A.购买一张彩票,中奖B.射击运动员射击一次,命中靶心
C.任意画一个三角形,其内角和是180°D.经过有交通信号灯的路口,遇到红灯
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
(1)请直接写出点A关于原点O对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com