
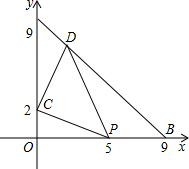
 如图,在△AOB中,OA=0B=9,点C的坐标为(0,2),点P是OB上一动点,连接CP,将CP绕C点逆时针旋转90°得到线段CD,使点D恰好落在AB上,求点D的坐标.
如图,在△AOB中,OA=0B=9,点C的坐标为(0,2),点P是OB上一动点,连接CP,将CP绕C点逆时针旋转90°得到线段CD,使点D恰好落在AB上,求点D的坐标.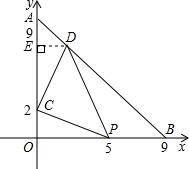 解:如图,过点D作DE⊥OA于E,
解:如图,过点D作DE⊥OA于E,
|


科目:初中数学 来源: 题型:
 如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( )
如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备
某居民区一处圆形下水管道破裂,维修人员准备更换一段新管道,如图,污水水面宽度为60cm,水面到管道顶部距离为10cm,则修理人员应准备查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com