
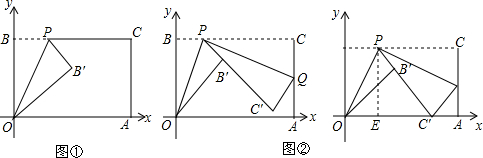
分析 (1)过点B′作B′D⊥OA于点D,由条件证得∠B'DO=45°,而OB'=6,则可直接算出B'的坐标;
(2)先由翻折性质推出∠OPQ=90°,进而推出△OBP∽△PCQ,列出相似比例关系即可;
(3)过点P作PE⊥OA于E,易证△PC′E∽△C′QA,从而列出相似比例等式,注意到△PC′E≌△OC′B′,得出线段相等关系,将用到的线段用t或m表示出来代入相似比例关系等式中,结合(2)中结论消去m,得到关于t的一元二次方程,解之即可.
解答 解:(1)过点B′作B′D⊥OA于点D,如图,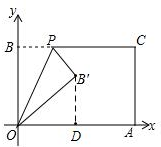
由翻折得△BOP≌△B′OP,
∴∠B′OP=∠BOP=22.5°,
∴∠B′OD=90°-∠B′OP-∠BOP=45°,
∵∠B'DO=90°,
∴∠B′OD=∠O B′D=45°,
∴OD=B′D 且设OD=B′D=a,
由勾股定理得 a2+a2=62,$a=3\sqrt{2}$,
∴点B′的坐标为$(3\sqrt{2},3\sqrt{2})$;
(2)如图,
∵△OB′P、△QC′P分别是由△OBP、△QCP折叠得到的,
∴△OB′P≌△OBP,△QC′P≌△QCP,
∴∠OPB′=∠OPB,∠QPC′=∠QPC,
∵∠OPB′+∠OPB+∠QPC′+∠QPC=180°,
∴∠OPB+∠QPC=90°,
∵∠BOP+∠OPB=90°,
∴∠BOP=∠CPQ,
又∵∠OBP=∠C=90°,
∴△OBP∽△PCQ,∴$\frac{OB}{PC}=\frac{BP}{CQ}$,
由题意设BP=t,AQ=m,BC=11,AC=6,则PC=11-t,CQ=6-m.∴$\frac{6}{11-t}=\frac{t}{6-m}$
∴$m=\frac{1}{6}{t^2}-\frac{11}{6}t+6$(0<t<11).
(3)过点P作PE⊥OA于E,如图,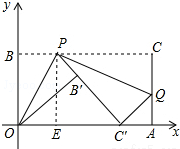
∴∠PEA=∠QAC′=90°,
∴∠PC′E+∠EPC′=90°,
∵∠PC′E+∠QC′A=90°,
∴∠EPC′=∠QC′A,
∴△PC′E∽△C′QA,
∴$\frac{{P{E^{\;}}}}{{A{C^′}}}=\frac{{E{C^′}}}{AQ}$,
在△PC′E和△OC′B′中,
$\left\{\begin{array}{l}{PE=OB'}\\{∠PEC'=∠OB'C}\\{∠PC'E=∠OC'B'}\end{array}\right.$,
∴△PC′E≌△OC′B′,
∴PC'=OC'=PC,
∴BP=AC',
∵AC′=PB=t,PE=OB=6,AQ=m,EC′=11-2t,
∴$\frac{6}{t}=\frac{11-2t}{m}$,
∵$m=\frac{1}{6}{t^2}-\frac{11}{6}t+6$,
∴3t2-22t+36=0,
解得:${t_1}=\frac{{11-\sqrt{13}}}{3},{t_2}=\frac{{11+\sqrt{13}}}{3}$.
故点P的坐标为($\frac{{11-\sqrt{13}}}{3}$,6)或($\frac{{11+\sqrt{13}}}{3}$,6).
点评 本题考查了翻折变换的性质、矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、解一元二次方程等知识点,综合性较强,难度较大.清楚翻折前后的两个图形全等以及熟悉相似三角形的判定与性质是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
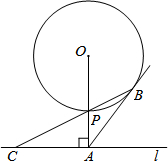 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
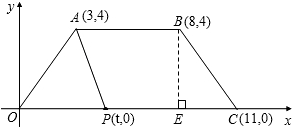 如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com